Aprenda Programação: Aritmética e Matemática Básica
Créditos para a imagem: Imagem criada pelo autor usando o programa Spectacle.
Pré-Requisitos
Na introdução sobre ambientes de desenvolvimento, indiquei Python, Lua e JavaScript como boas escolhas de linguagens de programação para iniciantes. Posteriormente, comentei sobre GDScript como opção para pessoas que tenham interesse em programar jogos digitais ou simulações. Para as atividades de introdução a programação, você precisará de, no mínimo, um ambiente de desenvolvimento configurado em uma das linguagens anteriores.
Caso queira experimentar programação sem configurar um ambiente, você pode usar um dos editores online que criei:
Contudo, eles não possuem todos os recursos dos interpretadores para as linguagens. Assim, cedo ou tarde, você precisará configurar um ambiente de desenvolvimento. Caso precise configurar um, confira os recursos a seguir.
Assim, se você tem um Ambiente Integrado de Desenvolvimento (em inglês, Integrated Development Environment ou IDE) ou a combinação de editor de texto com interpretador, você está pronto para começar. Os exemplos assumem que você saiba executar código em sua linguagem escolhida, como apresentado nas páginas de configuração.
Caso queira usar outra linguagem, a introdução provê links para configuração de ambientes para as linguagens C, C++, Java, LISP, Prolog e SQL (com SQLite). Em muitas linguagens, basta seguir os modelos da seção de experimentação para adaptar sintaxe, comandos e funções dos trechos de código. C e C++ são exceções, por requerem o uso de ponteiros para acesso à memória.
Operações Matemáticas para Programação
Operações aritméticas estão entre as operações mais básicas que computadores podem fazer. De fato, um dos componentes do processador chama-se Unidade Lógico-Aritmética (ULA em Português, ou Arithmetic Logic Unit ou ALU, em Inglês). Em uma metáfora com o corpo humano, a ULA corresponderia ao cérebro da máquina. Se o termo aritmética faz parte do cérebro, parece justo supor que seja importante para programação.
Operações Básicas
Computadores podem fazer todas as operações aritméticas básicas: somas, subtrações, multiplicações e divisões. Linguagens de programação também fornecem operadores ou subrotinas (funções ou procedimentos) para potenciações e radiciações.
| Operação | Operador Usual |
|---|---|
| Soma | + |
| Subtração | - |
| Multiplicação | * |
| Divisão | / |
A divisão requer atenção. Não apenas porque o divisor não pode ser zero, mas também porque existem dois tipos:
- Divisão real: divisão na qual, ao menos, um dos operandos é um número real. A divisão real resulta em um número real, com resultado aproximado (caso a divisão não seja exata). Por exemplo, .
- Divisão inteira: divisão na qual ambos os operandos são números inteiros.
A divisão inteira sempre resulta em um número inteiro.
Caso a divisão não seja exata, ela tem resto.
É comum que linguagens de programação definam um operador especial para obtenção do resto de divisão inteira.
Operadores usuais incluem
%oumod. Por exemplo, (parte inteira); (resto; a divisão de 5 por 2 tem resto 1).
Existem linguagens de programação que definem dois operadores para divisão: um para divisão real (como /), outro para divisão inteira (como \ ou //).
Em linguagens de programação que definem um único operador para divisão, a convenção usual é que a divisão de dois números inteiros é uma divisão inteira.
Qualquer divisão em que ao menos um dos operandos for um número real é uma divisão real.
Por isso, é importante escrever números como 2.0 para assegurar a realização de divisões reais.
Outro benefício é que explicitar o .0 facilita a explicação da intenção de realizar divisão real para outras pessoas que lerem o código-fonte.
Operações Avançadas
Além das operações básicas, linguagens de programação comumente fornecem recursos para trigonometria, probabilidade e estatística. Algumas linguagens de programação também fornecem recursos para, dentre outros, álgebra, geometria e topologia.
Além de Matemática pura, pode-se usar operações para Matemática aplicada. Por exemplo, pode-se criar simulações, cálculos e processamentos físicos, e modelagens gráficas (usando recursos como matrizes).
A Aposentadoria da Calculadora e das Planilhas de Cálculo
Computadores são máquinas muito mais poderosas, capazes e flexíveis que calculadoras. Conhecendo o básico de uma linguagem de programação, pode-se aposentar calculadoras tradicionais. Conhecendo um pouco mais sobre programação, pode-se aposentar programas de planilhas de cálculo, como LibreOffice Calc e Microsoft Excel.
A maioria das linguagens de programação permite fazer tudo que calculadoras e planilhas de cálculo permitem, sem as limitações impostas pelas tecnologias anteriores. Ou seja, uma linguagem de programação faz de computadores ferramentas para Matemática.
Assim como linguagens de programação, você poderá escolher a ferramenta mais adequada para a resolução de problemas. Para problemas simples, ela pode ser uma calculadora. Para problemas mais complexos, talvez uma planilha de cálculos. Para quaisquer dos problemas anteriores e problemas mais complexos, o computador tende a tornar-se uma melhor opção.
Aritmética Digital
A Matemática cotidiana comumente utiliza números decimais, isto é, números com base 10. A Matemática digital utiliza números binários, isto é, números com base 2.
Todos os valores processados por computadores são codificados como seqüências de dígitos binários.
As subseções a seguir comentam rapidamente sobre codificação numérica para computadores. As linguagens de programação fazem as conversões automaticamente; assim, o conteúdo é ilustrativo, para ajudar você a entender um pouco mais sobre o funcionamento de computadores.
Aritmética de Números Inteiros
Em Tipos de Dados, comentou-se sobre a escolha de números inteiros para operações que requeiram precisão. Neste momento, convém entender um pouco mais sobre eles.
A codificação de números naturais em sistemas digitais é imediata, pois pode ser representada como somas de potenciações com base 2. Uma seqüência de bits pode codificar valores naturais distintos. Por padrão, considera-se que a seqüência comece de zero, pois esse é o valor do primeiro número natural. Os valores compreendem o intervalo iniciado em até , ou seja, .
Assim, caso se decida representar números usando 4 bits, pode-se escrever números entre a (). A tabela a seguir lista todos os possíveis valores com representação binária de 4 bits. Para entender a terceira coluna da tabela, é mais simples visualizar a representação binária com adição de zeros à esquerda do número, para completar o 4 bits.
| Decimal | Binário | Binário (4 bits) |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 10 | 0010 |
| 3 | 11 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | 1000 |
| 9 | 1001 | 1001 |
| 10 | 1100 | 1100 |
| 11 | 1101 | 1101 |
| 12 | 1100 | 1100 |
| 13 | 1101 | 1101 |
| 14 | 1110 | 1110 |
| 15 | 1111 | 1111 |
A escrita do valor 16 requereria um bit adicional, como apresentado na tabela a seguir. A inclusão do bit adicional permitiria escrever números de 0 até 31, efetivamente dobrando o total de possíveis valores.
| Decimal | Binário | Binário (5 bits) |
|---|---|---|
| 0 | 0 | 00000 |
| 1 | 1 | 00001 |
| 2 | 10 | 00010 |
| 3 | 11 | 00011 |
| 4 | 100 | 00100 |
| 5 | 101 | 00101 |
| 6 | 110 | 00110 |
| 7 | 111 | 00111 |
| 8 | 1000 | 01000 |
| 9 | 1001 | 01001 |
| 10 | 1100 | 01100 |
| 11 | 1101 | 01101 |
| 12 | 1100 | 01100 |
| 13 | 1101 | 01101 |
| 14 | 1110 | 01110 |
| 15 | 1111 | 01111 |
| 16 | 10000 | 10000 |
| 31 | 11111 | 11111 |
Para converter um valor de binário para decimal, multiplica-se cada dígito do número binário por uma potência de 2 correspondente e faz-se um somatório. O cálculo começa do dígito menos significativo (mais à direita) com multiplicação pela potência , até o dígito menos significativo (mais à esquerda) pela potência , sendo o número bits considerado.
| Decimal | Binário | Cálculo para Conversão de Binário para Decimal |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 10 | |
| 3 | 11 | |
| 4 | 100 | |
| 5 | 101 | |
| 6 | 110 | |
| 7 | 111 | |
| 8 | 1000 | |
| 9 | 1001 | |
| 10 | 1100 | |
| 11 | 1101 | |
| 12 | 1100 | |
| 13 | 1101 | |
| 14 | 1110 | |
| 15 | 1111 | |
| 16 | 10000 | |
| 31 | 11111 |
Números naturais em programação são comumente chamados de inteiros sem sinal. O termo é usado porque a codificação de um número inteiro (que também pode ser negativo) requer escolhas para codificação do sinal. Números inteiros com sinal ou, simplesmente, números inteiros devem representar o sinal em codificação binária. Existem duas escolhas comuns para codificação de números inteiros:
- Usar um bit para sinal;
- Usar complemento de dois.
Linguagens de programação costumam representar números inteiros em complemento de dois. O uso de complemento de dois permite realizar subtrações meio de somas e a representação de um valor adicional para uma determinada quantidade de bits.
Por exemplo, para inteiros de 8 bits (1 byte), a tabela a seguir relaciona a representação binária com valores codificados para número natural (inteiro sem sinal), inteiro com sinal usando bit de sinal, e inteiro com sinal usando complemento de 2. É interessante notar que uma mesma seqüencia binária pode ter várias interpretações. A interpretação para o significado depende da codificação e da decodificação adotada.
| Representação binária | Inteiro sem sinal | Inteiro com sinal (bit de sinal) | Inteiro com sinal (complemento de 2) |
|---|---|---|---|
| 00000000 | 0 | 0 | 0 |
| 00000001 | 1 | 1 | 1 |
| 00000010 | 2 | 2 | 2 |
| 01111111 | 127 | 127 | 127 |
| 10000000 | 128 | -0 | -128 |
| 10000001 | 129 | -1 | -127 |
| 10000010 | 130 | -2 | -126 |
| 11111110 | 254 | -126 | -2 |
| 11111111 | 255 | -127 | -1 |
Para atividades práticas de programação, é importante saber sobre a existência da codificação porque existem duas abordagens usuais para representar a precisão de números inteiros (que variam de linguagem para linguagem):
- Número inteiro com precisão fixa, que depende de um número fixo de bits usado para codificação;
- Número inteiro com precisão arbitrária, que permite o uso de uma quantidade variável de bits para codificação.
No caso de precisão fixa, existe um valor máximo e um valor mínimo para cada número considerado de bits para representação. Por exemplo, com um byte (8 bits), é possível representar 256 números (0 a 255 sem sinal; -128 a 127 em complemento de 2). Quanto maior o número de bits ou bytes usados para codificação, maior o intervalo de número que se pode representar. A tabela a seguir apresenta um sumário para quantidades de bits comumente usadas para números inteiros em linguagens de programação. O menor valor inteiro para números sem sinal sempre é zero.
| Numero de bits | Número de bytes | Maior inteiro (com sinal) | Menor inteiro (complemento de 2) | Maior inteiro (complemento de 2) |
|---|---|---|---|---|
| 1 | - | 1 | -1 | 0 |
| 8 | 1 | 255 | -128 | 127 |
| 16 | 2 | 65535 | -32768 | 32767 |
| 32 | 4 | 4294967295 | -2147483648 | 2147483647 |
| 64 | 8 | 18446744073709551615 | -9223372036854775808 | 9223372036854775807 |
Os números máximos e mínimos para 8, 16 e 32 bits (1, 2 e 4 bytes, respectivamente) são comuns em jogos digitais. Por exemplo, se você já jogou um Role-Playing Game (RPG) nos quais atributos variam de 0 a 255, ou de -128 a 127, o motivo é o armazenamento em uma variável do tipo inteiro com tamanho de um byte.
A tabela anterior ajuda a decidir sobre o tipo e tamanho de número inteiro que se deve adotar dependendo dos valores que se espera armazenar em uma variável do tipo inteiro. A escolha é importante porque somas (ou multiplicações) que excedam o valor máximo resultam em um resultado incorreto chamado de overflow. Da mesma forma, subtrações (ou multiplicações) que excedam o valor mínimo resultam em um resultado incorreto chamado de underflow. Os erros também são chamados de estouro de bits, porque o resultado requereria um número de bits para representação maior que o disponível. Na falta de um bit adicional, o erro manifesta-se no bit de sinal.
Overflow ou underflow ocorrem porque, tanto em bit de sinal, quanto em complemento de dois, o dígito mais significativo é usado como sinal. Caso uma operação altere o valor do dígito mais significativo, o sinal do resultado será invertido.
Uma forma simples de verificar se ocorreu um overflow consiste em comparar sinais. Caso se some (ou multiplique) dois números positivos e o resultado for negativo, sabe-se que o resultado está incorreto e que ocorreu overflow. Analogamente, caso se some dois números negativos e o resultado for positivo, sabe-se que o resultado está incorreto devido a um underflow.
A forma procede porque a soma ou multiplicação de dois números positivos também deve resultar em um número positivo. Da mesma forma, a soma de dois números negativos também deve resultar em um número negativo, assim como a multiplicação de um número positivo por um negativo (ou vice-versa).
Em linguagens de programação que adotem números inteiros com 4 bytes, a ocorrência de overflow e underflow é possível e provável, dependendo dos valores que serão utilizados. Em linguagens de programação que adotem números inteiros com 8 bytes, a ocorrência de overflow e underflow é improvável, exceto caso se trabalhe com números muito grandes ou pequenos. Contudo, improvável não é impossível; ela é possível e requer atenção para se evitar erros.
Algumas linguagens de programação oferecem números inteiros com precisão arbitrária, utilizando aritmética precisão arbitrária (arbitrary-precision arithmetic) (também chamada de big number ou bignum arithmetic). Em aritmética de precisão arbitrária, o número de bits para codificação é variável. Assim, na prática, a limitação de valores que podem ser armazenados dependem apenas da quantidade de memória livre disponível no sistema.
Aritmética de Números Reais
A aritmética para números reais tradicionalmente usada em computadores chama-se aritmética de ponto flutuante (ou vírgula flutuante). Como a representação de números em ponto flutuante é um pouco mais complexa que a de números inteiros, o restante da subseção foca em partes mais práticas.
O primeiro ponto que requer atenção é que nem sempre é possível representar a parte decimal de números reais com precisão usando números binários. Isso não é restrito apenas à valores como números irracionais ou dízimas periódicas, mas também a qualquer número decimal que não possa ser escrito como soma de potências com expoentes negativos 2.
Enquanto a parte inteira é composta por somas de potências de dois (), a parte decimal é composta por somatórios do inverso da razão de potências de dois ( = ). Isso significa que números como ou () podem ser escritos com o valor exato em representação binária. Por outro lado, o número não pode, pois ele apenas pode ser aproximado (). Para se obter os termos, soma-se novos valores que não excedam o valor considerado (, nesse caso), ignorando-se os demais. Quanto mais valores usados para a aproximação, maior será a precisão; contudo, o valor nunca será exato.
O segundo ponto de atenção é que a precisão de aritmética de ponto flutuante é limitada. Isso significa que todo cálculo usando números flutuantes é suscetível a potenciais erros de aproximação (ou mesmo valores incorretos).
Embora a margem de erro possa ser pequena (e, potencialmente, desprezível) em alguns casos, operações sucessivas com valores aproximados estão sujeitas a erros acumulados. Em outras palavras, erros que poderiam ser desprezíveis no início podem tornar-se cada vez mais significativos.
Portanto, quando precisão for fundamental para um problema, pode ser mais interessante usar números inteiros a usar ponto-flutuante. Outras opção é usar codificações alternativas para números reais. Um exemplo de codificação alternativa chama-se codificação binária decimal (do inglês, binary-coded decimal ou BCD), que é usada para cálculos financeiros e industriais. BCD é menos eficiente que ponto-flutuante quanto ao uso de memória e do processador, mas é mais precisa (por codificar cada dígito de um número individualmente).
Precedência de Operadores
Assim como na Matemática, operadores em programação podem possuir diferentes prioridades quando avaliados em expressões. Como na Matemática, normalmente também é possível alterar a ordem de avaliação de expressões usando-se parênteses. Expressões com parênteses possuem a maior prioridade para avaliação.
De forma geral, em ordem decrescente de precedência:
- Agrupamento: expressões entre parênteses (
()) possuem a maior prioridade para avaliação; - Chamada de subrotina (função, procedimento, método), exponenciação;
- Multiplicação, divisão e resto;
- Adição, subtração;
- Atribuição.
Da lista anterior, itens que aparecem antes são avaliados antes dos que aparecem depois. Isso significa que uma expressão como:
x = 1 - 2 * 3 / 4.0
Resulta em -0.5, pois é calculada como:
x = 1 - ((2 * 3) / 4.0)
Cabe lembrar que, no exemplo, o igual (=) é uma atribuição, não uma igualdade.
A avaliação corresponde à avaliação da Matemática cotidiana, pois a expressão correspondente seria:
Na equação, o igual é uma igualdade, não uma atribuição.
Resolvendo a expressão passo a passo (como um computador):
Pessoalmente, eu prefiro usar parênteses mesmos em situações nas quais não são necessários, por facilitar a leitura da expressão. É muito mais fácil identificar as operações que ocorrem antes no exemplo com parênteses do que no exemplo sem.
Matemática em Programação
Como habitual, a introdução teórica é mais complexa que o uso de aritmética em programação. As próximas seções exemplificam como usar operações matemáticas na prática.
Fluxogramas: Flowgorithm
Em Flowgorithm, os operadores usados para aritmética são:
- Soma:
+; - Subtração:
-; - Multiplicação:
*; - Divisão:
/; - Resto de divisão:
%oumod; - Potenciação:
^.
Pode-se encontrar mais detalhes na documentação.
Para se calcular raízes quadradas, é possível usar sqrt().

O bloco a seguir contém a transcrição do texto da imagem.
Principal
Inteiro soma
soma = 1 + 2
Saída soma
Inteiro subtracao
subtracao = 1 - 2
Saída subtracao
Inteiro multiplicacao
multiplicacao = 1 * 3
Saída multiplicacao
Inteiro divisaoInteira
divisaoInteira = 9 / 4
Saída divisaoInteira
Inteiro restoDivisaoInteira
restoDivisaoInteira = 9 % 4
Saída restoDivisaoInteira
Real divisaoReal
divisaoReal = 9 / 4
Saída divisaoReal
Inteiro potenciacao
potenciacao = 10 ^ 5
Saída potenciacao
Real raizQuadrada
raizQuadrada = sqrt(9)
Saída raizQuadrada
Real raizCubica
raizCubica = 1000 ^ (1.0 / 3.0)
Saída raizCubica
Real x
x = 1 - ((2 * 3) / 4.0)
Saída x
FimPara armazenar um resultado, pode-se usar o bloco de Atribuição (Assign).
A escolha do tipo de resultado é feita de acordo com o tipo da variável que armazenará o resultado. Se a variável for real, o resultado calculado também será real. Assim, para se fazer uma divisão inteira, é preciso usar uma variável do tipo inteiro.
Linguagens de Programação Visual: Scratch
Em Scratch, operadores aritméticos e funções matemáticas estão em Operadores (Operators).
Para operadores aritméticos básicos, cada operação é representada por seu símbolo (+, -, *, /).
Para o resto de divisão, pode-se usar o operador resto de _ por _ (_ mod _).
Para outras operações, deve-se usar o bloco módulo de _ (abs of ``_) e trocar _módulo__ por:
- Para potenciação: 10 elevado 1 à
_(10 ^_; para base 10) ou por e elevado à_(e ^_; para base com número de Euler -- aproximadamente 2,71828182); - Para raiz quadrada: raiz quadrada (sqrt);
- Para arredondamento para baixo para divisão inteira: arredondamento para baixo de
_(floor of_).
Uma limitação dos blocos fornecidos por padrão é a falta de suporte para potenciação por bases diferentes de 10 ou . Para simplificar o exemplo, o programa em Scratch faz um cálculo de raiz cúbica diferente dos demais desta página ( ao invés de ).
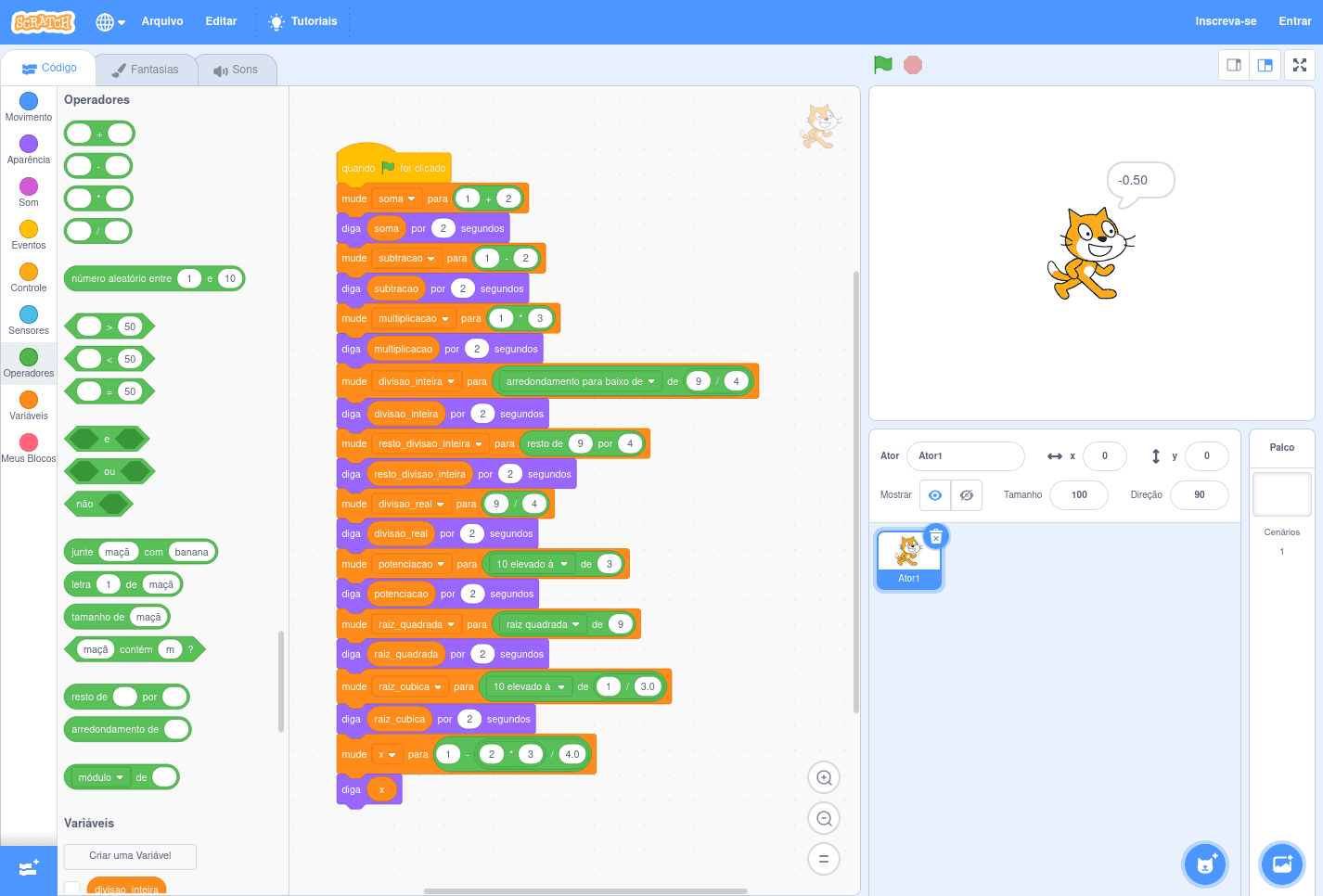
Com o uso de Matemática um pouco mais avançada, é possível calcular valores para outras bases. Para bases não negativas, uma alternativa é usar propriedades de logaritmos para mudanças de base. Para as bases fornecidas, pode-se usar logaritmo em base 10 para potências de 10:
Ou o logaritmo natural (ou neperiano) para potências de :
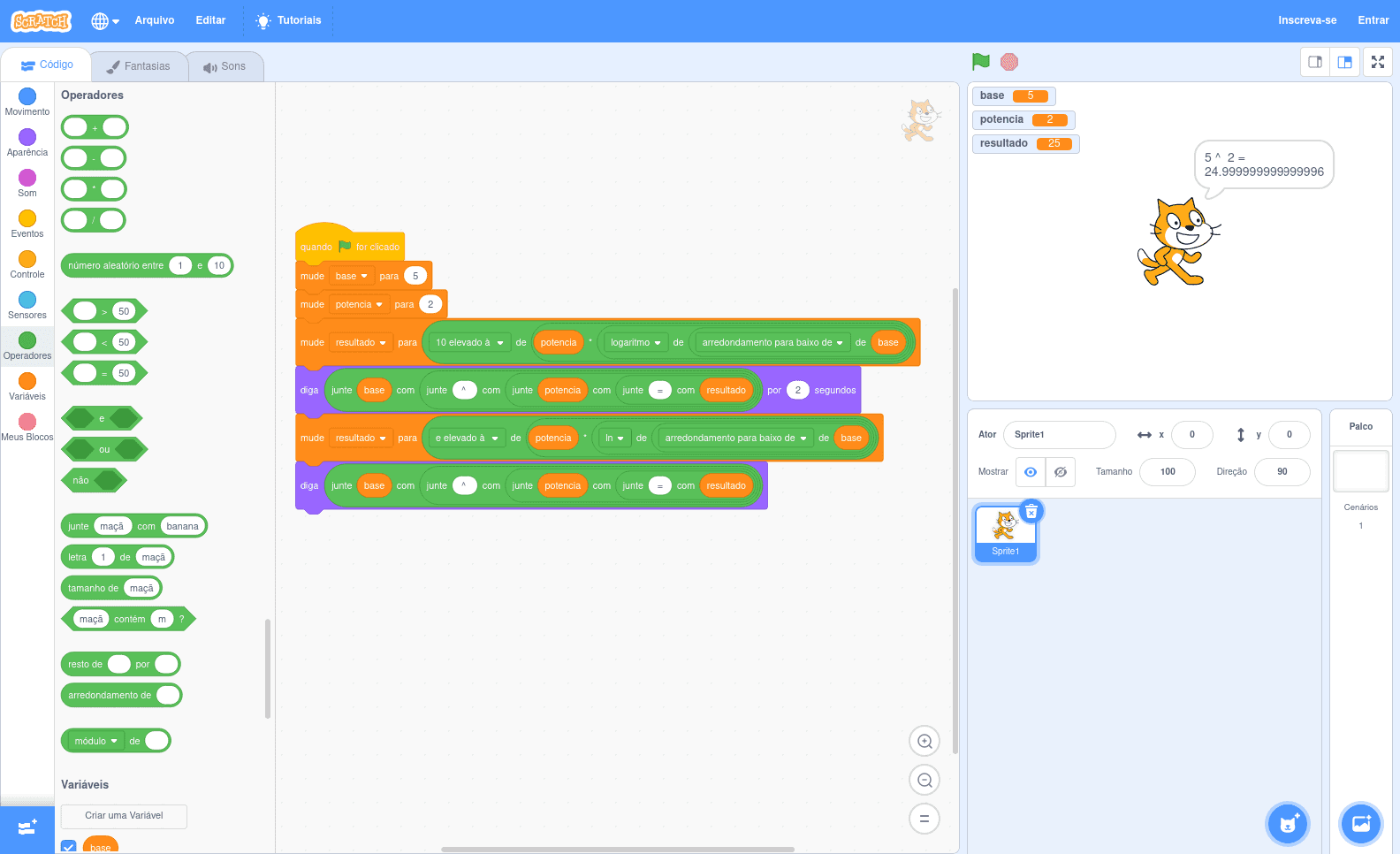
A maioria das linguagens de programação fornecem comandos ou funções para cálculos de potenciação, então o exemplo é meramente ilustrativo.
Linguagens de Programação Textual: JavaScript, Python, Lua e GDScript
Antes de começar a calcular expressões matemáticas em linguagens de programação, convém consultar a documentação sobre precedência de operadores.
- JavaScript: documentação;
- Python: documentação;
- Lua: documentação;
- GDScript: documentação.
Operações Aritméticas Básicas
Os blocos de código a seguir apresentam exemplos de realização de soma, subtração, multiplicação, divisão inteira, resto de divisão inteira, divisão real, potenciação e radiciação em JavaScript, Python, Lua e GDScript. Em seguida, utiliza-se o exemplo fornecido no texto com uma expressão usando parênteses. Por fim, fornece-se um último exemplo com o uso de variáveis como operandos de uma operação aritmética.
let soma = 1 + 2
console.log(soma)
let subtracao = 1 - 2
console.log(subtracao)
let multiplicacao = 1 * 3
console.log(multiplicacao)
let divisao_inteira = Math.floor(9 / 4)
console.log(divisao_inteira)
let resto_divisao_inteira = 9 % 4
console.log(resto_divisao_inteira)
let divisao_real = 9 / 4
console.log(divisao_real)
let potenciacao = Math.pow(10, 5)
console.log(potenciacao)
// Em navegadores modernos:
potenciacao = 10 ** 5
console.log(potenciacao)
let raiz_quadrada = Math.sqrt(9)
console.log(raiz_quadrada)
let raiz_cubica = Math.pow(1000, 1.0 / 3.0)
console.log(raiz_cubica)
// Exemplo de expressão.
let x = 1 - ((2 * 3) / 4.0)
console.log(x)
x = x + x
console.log(x)soma = 1 + 2
print(soma)
subtracao = 1 - 2
print(subtracao)
multiplicacao = 1 * 3
print(multiplicacao)
divisao_inteira = 9 // 4
print(divisao_inteira)
resto_divisao_inteira = 9 % 4
print(resto_divisao_inteira)
divisao_real = 9 / 4
print(divisao_real)
potenciacao = 10 ** 5
print(potenciacao)
import math
raiz_quadrada = math.sqrt(9)
print(raiz_quadrada)
raiz_cubica = 1000 ** (1.0 / 3.0)
print(raiz_cubica)
# Exemplo de expressão.
x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)local soma = 1 + 2
print(soma)
local subtracao = 1 - 2
print(subtracao)
local multiplicacao = 1 * 3
print(multiplicacao)
local divisao_inteira = 9 // 4 -- Requer Lua 5.3 ou mais recente.
print(divisao_inteira)
divisao_inteira = math.floor(9 / 4) -- Alternativa para versões anteriores.
print(divisao_inteira)
local resto_divisao_inteira = 9 % 4
print(resto_divisao_inteira)
local divisao_real = 9 / 4
print(divisao_real)
local potenciacao = 10 ^ 5
print(potenciacao)
local raiz_quadrada = math.sqrt(9)
print(raiz_quadrada)
local raiz_cubica = 1000 ^ (1.0 / 3.0)
print(raiz_cubica)
-- Exemplo de expressão.
local x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)extends Node
func _ready():
var soma = 1 + 2
print(soma)
var subtracao = 1 - 2
print(subtracao)
var multiplicacao = 1 * 3
print(multiplicacao)
var divisao_inteira = 9 / 4
print(divisao_inteira)
var resto_divisao_inteira = 9 % 4
print(resto_divisao_inteira)
var divisao_real = 9 / 4.0
print(divisao_real)
var potenciacao = pow(10, 5)
print(potenciacao)
var raiz_quadrada = sqrt(9)
print(raiz_quadrada)
var raiz_cubica = pow(1000, (1.0 / 3.0))
print(raiz_cubica)
# Exemplo de expressão.
var x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)Das linguagens anteriores, GDScript distingüe divisões inteiras de divisões reais baseando-se no tipo de operandos.
Por isso, a divisão real é feita com 9 / 4.0 ao invés de 9 / 4.
As operações matemáticas anteriores são usadas com freqüência em programação. Em particular, o uso de variáveis para armazenar resultados intermediários é bastante comum. Utilizando bons nomes para variáveis, é possível auxiliar na leitura e no entendimento do código criado.
Incremento, Decremento e Operação com Atribuição
Por conveniência, linguagens de programação comumente fornecem uma combinação do operador de atribuição com um operador aritmético. Os principais costumam ser:
+=,-=,*=,/=, e%=:x += 1corresponde ax = x + 1;x -= 2corresponde ax = x - 2;x *= 3corresponde ax = x * 3;x /= 4corresponde ax = x / 4.
Os operadores anteriores costumam funcionar para qualquer tipo numérico. Em algumas linguagens de programação, o operador
+=usando com cadeias de caracteres realiza concatenação.++e--: incremento ou decremento de uma unidade (normalmente apenas para valores inteiros). Por exemplo:- Pré-incremento:
++x; - Pós-incremento:
x++; - Pré-decremento:
--x; - Pós-decremento:
x--.
A diferença entre pré e pós é a ordem na qual a operação é feita e o resultado é retornado. Em operações pré, a operação é feita antes do retorno do resultado. Por exemplo, em JavaScript:
x = 0 y = ++x console.log(x, y) // x = 1, y = 1Em operações pós, o resultado é retornado antes do cálculo da operação. Utilizando JavaScript novamente para um exemplo:
x = 0 y = x++ console.log(x, y) // x = 1, y = 0Muitas vezes, utiliza-se a operação em uma linha de código própria, com o resultado ignorado. Nesse caso, o uso é indiferente. Alguns compiladores ou interpretadores podem gerar código diferente para os dois, mas, muitas vezes, a otimização feita pela ferramenta gera código equivalente.
- Pré-incremento:
Nem toda linguagem de programação fornece os operadores ++ e --.
Por exemplo, Python e GDScript não definem nenhum dos dois operadores.
A substituição é simples: basta usar += 1 e -= 1, respectivamente.
Da mesma forma, algumas linguagens de programação (como Lua) não fornecem nenhum dos operadores anteriores.
Assim, toda operação deve ser feita explicitamente; por exemplo, x = x + 1.
let i = 0
console.log(i)
++i // i = i + 1
console.log(i)
i++ // i = i + 1
console.log(i)
i += 1 // i = i + 1
console.log(i)
i -= 2 // i = i - 2
console.log(i)
i *= 3 // i = i * 3
console.log(i)
i /= 4.0 // i = i / 4.0
console.log(i)i = 0
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i -= 2 # i = i - 2
print(i)
i *= 3 # i = i * 3
print(i)
i /= 4.0 # i = i / 4.0
print(i)local i = 0
print(i)
i = i + 1
print(i)
i = i + 1
print(i)
i = i + 1
print(i)
i = i - 2
print(i)
i = i * 3
print(i)
i = i / 4.0
print(i)extends Node
func _ready():
var i = 0
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i -= 2 # i = i - 2
print(i)
i *= 3 # i = i * 3
print(i)
i /= 4.0 # i = i / 4.0
print(i)Recursos para programação como as anteriores são, por vezes, chamadas de syntactic sugar (algo como açúcar sintático). Elas são conveniências providas pela linguagem para agilizar atividades freqüentes de programação.
Menores e Maiores Valores Inteiros
Python 3 é uma linguagem que utiliza números inteiros de precisão arbitrária.
Contudo, Python 2 não fornece.
Em Python 2, o maior número inteiro pode ser determinado usando-se sys.maxsize (requer import sys).
O menor pode ser descoberto com -sys.maxsize - 1.
JavaScript e Lua possuem limites para números inteiros (que são codificados como números reais internamente).
Em JavaScript, é possível consultar o maior valor que se pode representar usando-se Number.MAX_SAFE_INTEGER.
O menor número pode ser consultado usando-se Number.MIN_SAFE_INTEGER.
Em Lua, o maior número inteiro é fornecido por math.maxinteger; o menor número inteiro é acessível usando-se math.mininteger.
Em GDScript, números inteiros são codificados como inteiros com 64-bit com sinal.
let int_min = Number.MIN_SAFE_INTEGER
let int_max = Number.MAX_SAFE_INTEGER
console.log(int_min)
console.log(int_max)import sys
int_min = -sys.maxsize - 1
int_max = sys.maxsite
print(int_min)
print(int_max)local int_min = math.mininteger
local int_max = math.maxinteger
print(int_min)
print(int_max)extends Node
func _ready():
# O valor -9223372036854775808 não pode ser atribuído diretamente.
var int_min = -9223372036854775807 - 1
var int_max = 9223372036854775807
print(int_min)
print(int_max)Exemplos
Com as operações aritméticas anteriores, já é possível resolver diversos problemas do cotidiano usando programação. Também é possível resolver vários problemas de Matemática e Física do ensino fundamental e do médio.
Movimento Retilíneo Uniformemente Variado
Não é necessário ser especialista em Física para implementar equações existentes. Basta observar os símbolos e operadores, para, então, definir variáveis para os símbolos e escrever expressões combinando as variáveis com os operadores da linguagem de programação adotada.
Função Horária da Velocidade
Com:
- e em m/s (metros por segundo);
- em m/s²;
- em s. Tecnicamente, trata-se de um intervalo de tempo (ou seja, seria uma representação mais apropriada).
Você pode escolher os nomes que quiser para as variáveis.
Por exemplo, elas poderiam chamar vf, v0, a e t, para um código semelhante ao da equação.
Caso não queira lembrar o que cada símbolo significa no futuro, elas também poderiam ter os nomes velocidade_inicial, aceleracao, tempo e velocidade_final.
A implementação pode ser feita em qualquer linguagem de programação.
Como todos os valores podem ser números reais, o tipo mais adequado para variáveis é real.
Em particular, a escolha de tipos inteiros pode levar a resultados incorretos caso o resultado da expressão não seja um número inteiro.
Por exemplo, um resultado como 1.5 corresponderia a 1,5 m/s, mas o resultado obtido seria 1 m/s.
Nos exemplos a seguir, os valores fornecidos para variáveis são arbitrários. Você pode alterá-los conforme quiser.
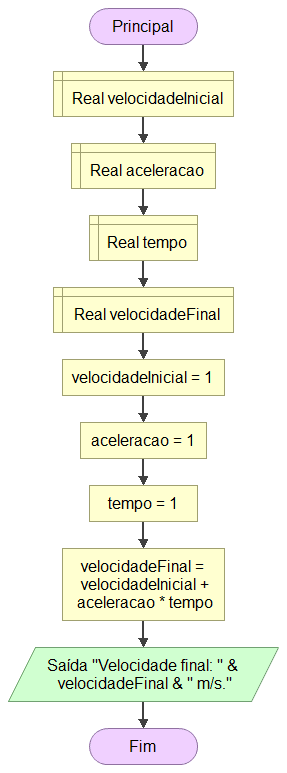
Principal
Real velocidadeInicial
Real aceleracao
Real tempo
Real velocidadeFinal
velocidadeInicial = 1
aceleracao = 1
tempo = 1
velocidadeFinal = velocidadeInicial + aceleracao * tempo
Saída "Velocidade final: " & velocidadeFinal & " m/s."
Fim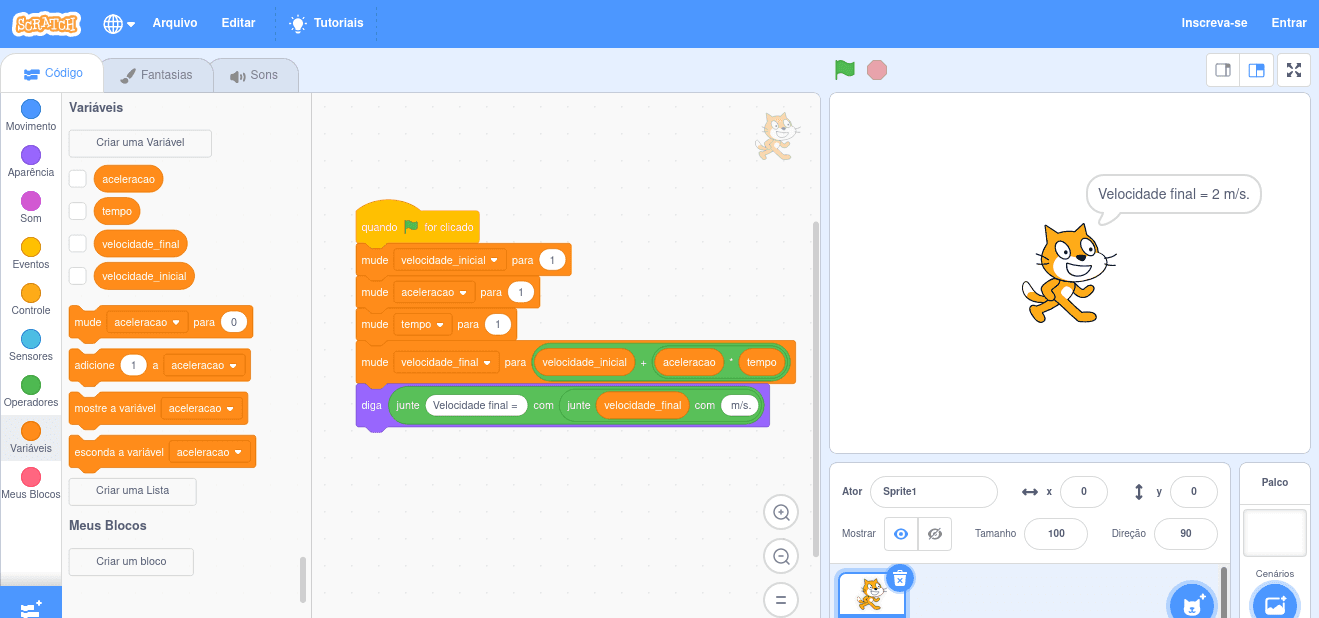
let velocidade_inicial = 1
let aceleracao = 1
let tempo = 1
let velocidade_final = velocidade_inicial + aceleracao * tempo
console.log("Velocidade final = ", velocidade_final, " m/s.")velocidade_inicial = 1
aceleracao = 1
tempo = 1
velocidade_final = velocidade_inicial + aceleracao * tempo
print("Velocidade final = ", velocidade_final, " m/s.")local velocidade_inicial = 1
local aceleracao = 1
local tempo = 1
local velocidade_final = velocidade_inicial + aceleracao * tempo
print("Velocidade final = ", velocidade_final, " m/s.")extends Node
func _ready():
var velocidade_inicial = 1
var aceleracao = 1
var tempo = 1
var velocidade_final = velocidade_inicial + aceleracao * tempo
print("Velocidade final = ", velocidade_final, " m/s.")Pessoalmente, eu recomendaria documentar no código-fonte as unidades esperadas para o cálculo. Neste caso, como a equação e as unidades estão próximas ao código, seria desnecessário. Contudo, em programas mais complexos, fornecer documentação no código-fonte para os parâmetros pode ser conveniente.
Você pode adicionar comentários sobre as unidades esperadas para cada variável. Por exemplo, escolhendo o código em JavaScript:
// Em m/s.
let velocidade_inicial = 1
// Em m/s².
let aceleracao = 1
// Em s.
let tempo = 1
// Cálculo da velocidade usando a função horária da velocidade.
// Em m/s.
let velocidade_final = velocidade_inicial + aceleracao * tempo
console.log("Velocidade final = ", velocidade_final, " m/s.")Outra possibilidade é incorporar as unidades aos nomes das varáveis:
let velocidade_inicial_m_s = 1
let aceleracao_m_s2 = 1
let tempo_s = 1
// Cálculo da velocidade usando a função horária da velocidade.
let velocidade_final_m_s = velocidade_inicial_m_s + aceleracao_m_s2 * tempo_s
console.log("Velocidade final = ", velocidade_final_m_s, " m/s.")Ambas as formas permitem entender o código-fonte com maior facilidade. Caso você (ou outra pessoa) precise alterá-lo no futuro, não seria necessário reler o código para inferir o funcionamento nem as unidades esperadas para uso correto do programa.
Além disso, é possível ler os parâmetros (por exemplo, usando entrada via console), ao invés de fixá-los no código-fonte. Para adaptar o código, você pode usar os conceitos estudados em Entrada em Console (Terminal). Por exemplo:
let velocidade_inicial_m_s = parseFloat(prompt("Velocidade inicial (m/s):"))
let aceleracao_m_s2 = parseFloat(prompt("Aceleração (m/s²):"))
let tempo_s = parseFloat(prompt("Tempo (s):"))
// Cálculo da velocidade usando a função horária da velocidade.
let velocidade_final_m_s = velocidade_inicial_m_s + aceleracao_m_s2 * tempo_s
console.log("Velocidade final = ", velocidade_final_m_s, " m/s.")
alert("Velocidade final = " + velocidade_final_m_s + " m/s.")velocidade_inicial_m_s = float(input("Velocidade inicial (m/s): "))
aceleracao_m_s2 = float(input("Aceleração (m/s²): "))
tempo_s = float(input("Tempo (s): "))
# Cálculo da velocidade usando a função horária da velocidade.
velocidade_final_m_s = velocidade_inicial_m_s + aceleracao_m_s2 * tempo_s
print("Velocidade final = ", velocidade_final_m_s, " m/s.")print("Velocidade inicial (m/s):")
local velocidade_inicial_m_s = io.read("*number")
print("Aceleração (m/s²):")
local aceleracao_m_s2 = io.read("*number")
print("Tempo (s): ")
local tempo_s = io.read("*number")
-- Cálculo da velocidade usando a função horária da velocidade.
velocidade_final_m_s = velocidade_inicial_m_s + aceleracao_m_s2 * tempo_s
print("Velocidade final = ", velocidade_final_m_s, " m/s.")Com a adição de entrada, o programa pode calcular a equação horária da velocidade para o movimento retilíneo uniformemente variado para quaisquer valores de velocidade inicial, aceleração e tempo. Contudo, como não há validação de entrada, seria possível fornecer valores incorretos para o programa, o geraria resultados incorretos.
Função Horária da Posição
Como :
Com:
- , e em m;
- em m/s;
- em s;
- em m/s².
Algo a atentar é que o resultado da divisão deve ser um número real. Assim, deve-se assegurar de que a divisão realizada será real ao invés de inteira. Caso contrário, resultados decimais serão arrendondados, incorretamente, para baixo.
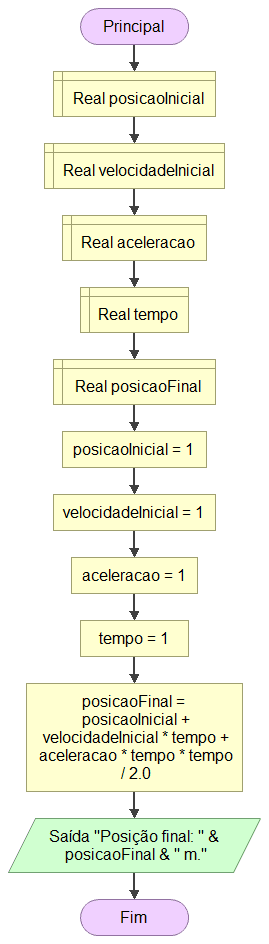
Principal
Real posicaoInicial
Real velocidadeInicial
Real aceleracao
Real tempo
Real posicaoFinal
posicaoInicial = 1
velocidadeInicial = 1
aceleracao = 1
tempo = 1
posicaoFinal = posicaoInicial + velocidadeInicial * tempo + aceleracao * tempo * tempo / 2.0
Saída "Posição final: " & posicaoFinal & " m."
Fim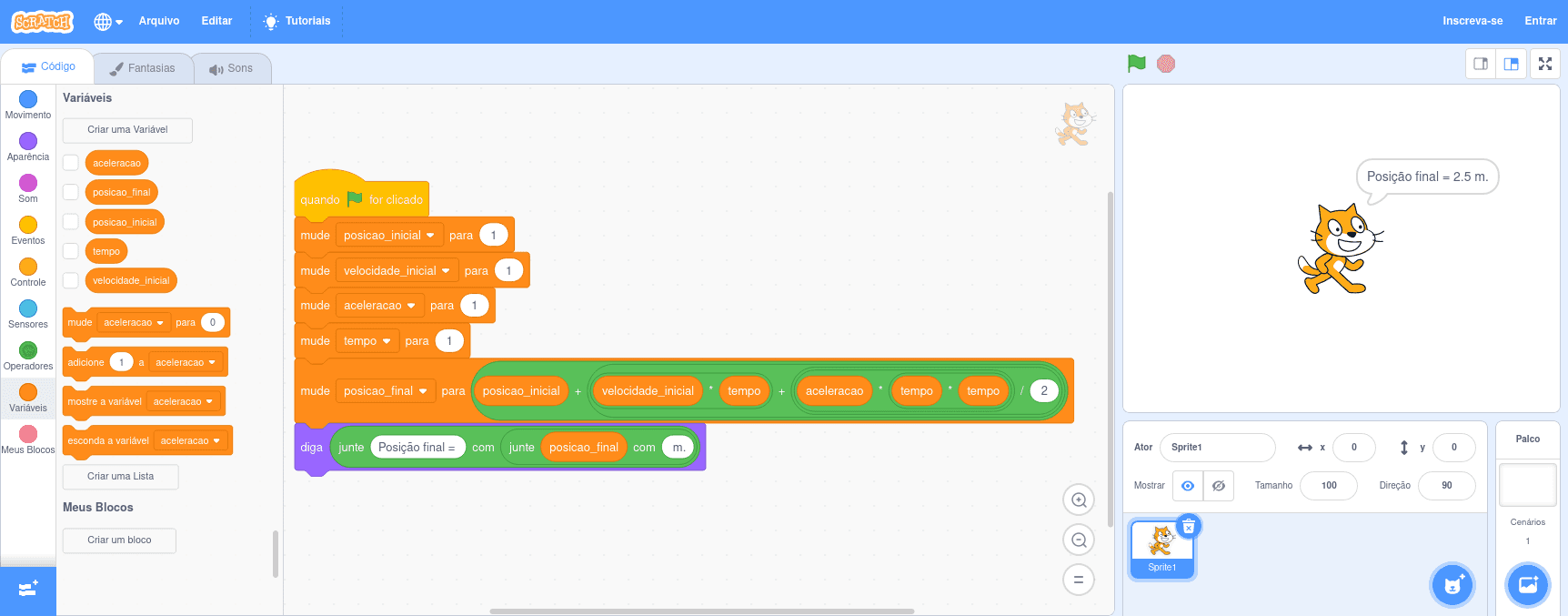
let posicao_inicial = 1
let velocidade_inicial = 1
let aceleracao = 1
let tempo = 1
let posicao_final = posicao_inicial + velocidade_inicial * tempo + aceleracao * tempo * tempo / 2.0
console.log("Posição final = ", posicao_final, " m.")posicao_inicial = 1
velocidade_inicial = 1
aceleracao = 1
tempo = 1
posicao_final = posicao_inicial + velocidade_inicial * tempo + aceleracao * tempo * tempo / 2.0
print("Posição final = ", posicao_final, " m.")local posicao_inicial = 1
local velocidade_inicial = 1
local aceleracao = 1
local tempo = 1
local posicao_final = posicao_inicial + velocidade_inicial * tempo + aceleracao * tempo * tempo / 2.0
print("Posição final = ", posicao_final, " m.")extends Node
func _ready():
var posicao_inicial = 1
var velocidade_inicial = 1
var aceleracao = 1
var tempo = 1
var posicao_final = posicao_inicial + velocidade_inicial * tempo + aceleracao * tempo * tempo / 2.0
print("Posição final = ", posicao_final, " m.")Os exemplos calculam o quadrado do tempo usando uma multiplicação, mas também seria possível usar uma potenciação e elevar o valor ao quadrado. O resultado seria o mesmo.
Para praticar, incorpore leitura de valores via console para as implementações em JavaScript, Python e Lua.
Cálculo de Potências com Logaritmos
O cálculo de potências usando logaritmos foi feito em Scratch. Para exemplos adicionais, pode-se implementá-los em outras linguagens de programação, como JavaScript, Python, Lua e GDScript.
Para isso, serão necessárias algumas funções adicionais, presentes na expressão. Em particular, funções para cálculo de:
- Módulo ou valor absoluto;
- Logaritmos na base 10;
- Logaritmos naturais, neperianos ou na base ;
- Uma função para cálculo de exponenciais -- ou simplesmente fazer .
Para isso, pode-se procurar pela constante
ena linguagem de programação ou usar um valor aproximado, como2.71828182.
Para procurar pelas funções necessárias, pode-se fazer buscas como "javascript mdn logaritmo" ou "javascript mdn logarithm" em motores de busca como Google, Bing ou DuckDuckGo.
- Módulo ou valor absoluto ():
- JavaScript
Math.abs(): documentação; - Python
abs(): documentação; - Lua
math.abs(): documentação; - GDScript:
abs(): documentação.
- JavaScript
- Logaritmo na base 10 ():
- JavaScript
Math.log10(): documentação; - Python
math.log10(): documentação; - Lua
math.log10(): documentação; - GDScript: não possui implementação pré-definida. O cálculo pode utilizar uma mudança de base.
- JavaScript
- Logaritmo na base ( ou ):
- JavaScript
Math.log(): documentação; - Python
math.log(): documentação; - Lua
math.log(): documentação; - GDScript:
log(): documentação.
- JavaScript
- Exponencial ():
- JavaScript
Math.exp(): documentação; - Python
math.exp(): documentação; - Lua
math.exp(): documentação; - GDScript:
exp(): documentação.
- JavaScript
Com as funções identificadas, pode-se implementar as soluções.
let base = 5
let potencia = 2
let resultado = Math.pow(10, potencia * Math.log10(Math.abs(base)))
console.log(resultado)import math
base = 5
potencia = 2
resultado = 10 ** (potencia * math.log10(abs(base)))
print(resultado)local base = 5
local potencia = 2
local resultado = 10 ^ (potencia * math.log10(math.abs(base)))
print(resultado)extends Node
func _ready():
var base = 5
var potencia = 2
var resultado = pow(10, potencia * log(abs(base)) / log(10))
print(resultado)GDScript é um caso particular, porque não fornece uma função para cálculo de logaritmos na base 10. Para resolver o problema, pode-se realizar uma mudança de base (). No exemplo anterior, fez-se .
let base = 5
let potencia = 2
let resultado = Math.exp(potencia * Math.log(Math.abs(base)))
console.log(resultado)import math
base = 5
potencia = 2
resultado = math.exp(potencia * math.log(abs(base)))
print(resultado)local base = 5
local potencia = 2
local resultado = math.exp(potencia * math.log(math.abs(base)))
print(resultado)extends Node
func _ready():
var base = 5
var potencia = 2
var resultado = exp(potencia * log(abs(base)))
print(resultado)Novos Itens para Seu Inventário
Ferramentas:
- Programação como calculadora;
- Programação como planilha de cálculo.
Habilidades:
- Cálculos matemáticos.
Conceitos:
- Divisão inteira;
- Resto de divisão inteira;
- Divisão real;
- Números inteiros com sinal;
- Números inteiros sem sinal;
- Underflow;
- Overflow;
- Números em ponto-flutuante;
- Erro acumulado;
- Precedência de operadores.
Recursos de programação:
- Operações ariméticas.
Pratique
Uma boa fonte de problemas matemáticos para programação é o Project Euler. Infelizmente, a página não possui traduções; todo o conteúdo está em Inglês. Além disso, muitos problemas requerem conceitos de programação ainda não explicados. Muitos requerem conceitos como estruturas de condição e de repetição, que ainda serão abordados.
Para uma introdução mais simples e uma alternativa disponível em vários idiomas é a lista de funções matemáticas da Wikipedia. As fórmulas mais simples são de geometria elementar.
Para começar, um dos recursos mais simples é a lista de fórmulas para cálculo de área de formas. Ainda mais simples é a lista de fórmulas para cálculo de perímetro, mas ela está disponível apenas em Inglês.
Também existe um sumário com uma lista de fórmulas da geometria elementar (apenas em Inglês).
Por conveniência, a tabela a seguir apresenta a tradução de algumas fórmulas para prática.
| Forma | Área | Perímetro | Comentário |
|---|---|---|---|
| Quadrado | é o tamanho de um lado | ||
| Retângulo | é o comprimento, é a largura | ||
| Círculo | é o raio | ||
| Triângulo | é a base; é a altura; , e são os lados | ||
| Trapézio | e são as bases; é a altura | ||
| Paralelogramo | é a base; é a altura; e são os lados |
| Forma | Volume | Área Superficial | Comentário |
|---|---|---|---|
| Cubo | é o tamanho de um lado | ||
| Prisma retangular | é o comprimento; é a altura; é a largura | ||
| Esfera | é o raio | ||
| Cilindro circular | é o raio; é a altura |
Convém salientar que, nas fórmulas, (lê-se pi) é um valor constante (aproximadamente 3.1415926).
Linguagens de programação comumente fornecem uma constante para .
Por exemplo:
- JavaScript:
Math.pi(documentação); - Python:
math.pi(documentação); - Lua:
math.pi(documentação); - GDScript:
math.pi(documentação);
Próximos Passos
Operações ariméticas são comuns em programação, mesmo quando não se resolva problemas de Matemática. Contudo, diferentemente de atividades escolares, o computador efetuará os cálculos e retornará os resultados. O papel da programadora ou do programador é, pois, definir as operações que devem ser feitas. Para isso, ela ou ele deve selecionar operadores e construir expressões em ordem adequada para precedência de operadores.
A vantagem de resolver um problema computacionalmente é poder usar a mesma solução para outros valores válidos. Como feito no exemplo como entrada, pode-se resolver o problema uma vez e aplicar a solução para outros valores pertencentes ao domínio do problema.
Como mencionado, operações matemáticas são parte da Unidade Lógico-Aritmética. A segunda parte que aparece no nome refere-se a operações lógicas e relacionais, cuja introdução inicia-se no próximo tópico.
- Introdução;
- Ponto de entrada e estrutura de programa;
- Saída (para console ou terminal);
- Tipos de dados;
- Variáveis e constantes;
- Entrada (para console ou terminal);
- Aritmética e Matemática básica;
- Operações relacionais e comparações;
- Operações lógicas e Álgebra Booleana;
- Estruturas de condição (ou condicionais ou de seleção);
- Subrotinas: funções e procedimentos;
- Estruturas de repetição (ou laços ou loops);
- Vetores (arrays), cadeias de caracteres (strings), coleções (collections) e estruturas de dados;
- Registros (structs ou records);
- Arquivos e serialização (serialization ou marshalling);
- Bibliotecas;
- Entrada em linha de comando;
- Operações bit-a-bit (bitwise operations);
- Testes e depuração.
