Learn Programming: Arithmetic and Basic Mathematics
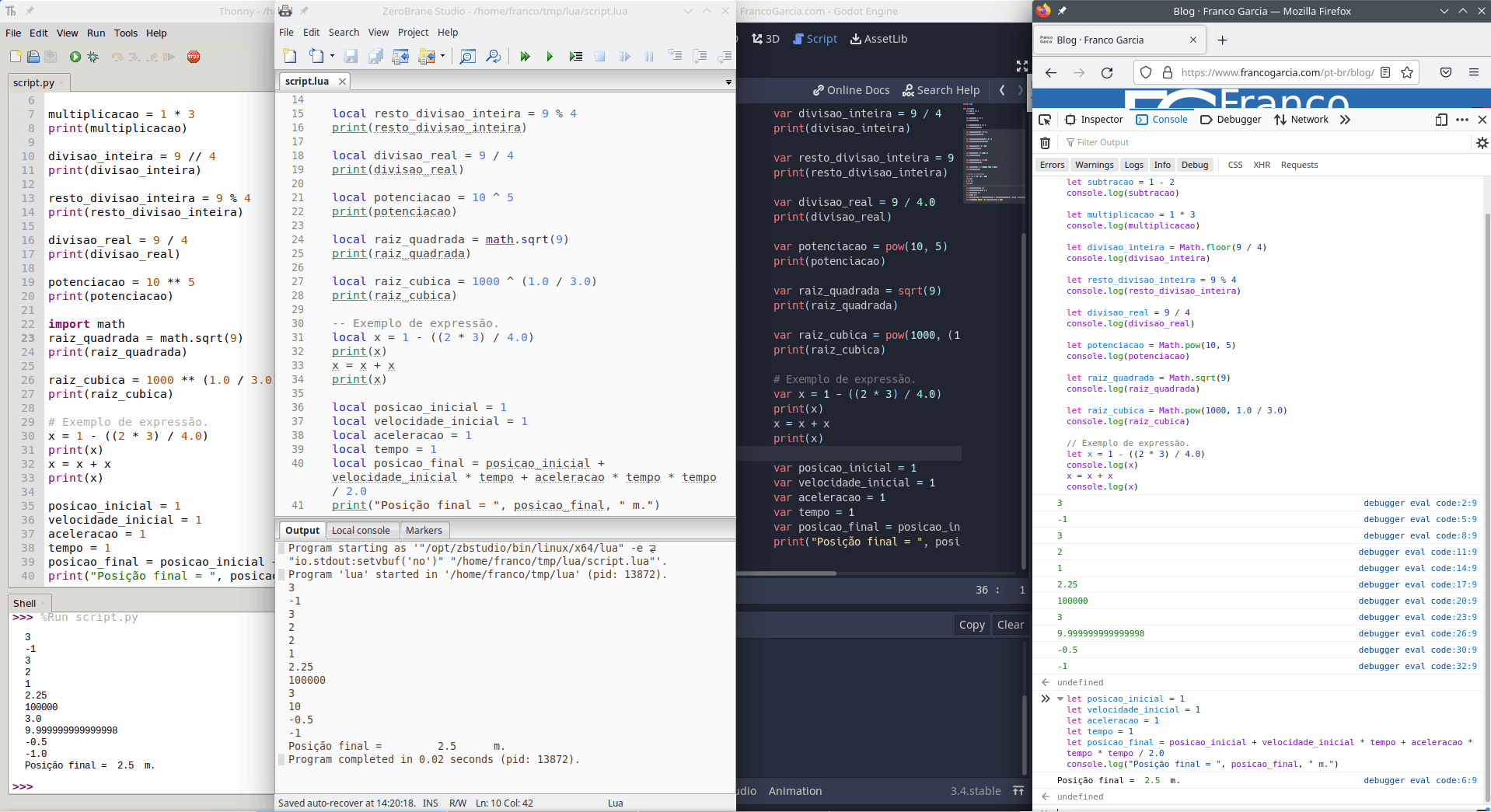
Image credits: Image created by the author using the program Spectacle.
Requirements
In the introduction to development environments, I have mentioned Python, Lua and JavaScript as good choices of programming languages for beginners. Later, I have commented about GDScript as an option for people who want to program digital games or simulations. For the introductory programming activities, you will need, at least, a development environment configured for one of the previous languages.
If you wish to try programming without configuring an environment, you can use of the online editors that I have created:
However, they do not provide all features offered by interpreters for the languages. Thus, sooner or later, you will need to set up a development environment. If you need to configure one, you can refer to the following resources.
Thus, if you have an Integrated Development Environment (IDE), or a combination of text editor and an interpreter, you are ready to start. The following example assumes that you know how to run code in your chosen language, as presented in the configuration pages.
If you want to use another language, the introduction provides links for configure development environments for the C, C++, Java, LISP, Prolog, and SQL (with SQLite) languages. In many languages, it suffices to follow the models from the experimentation section to modify syntax, commands and functions from the code blocks. C and C++ are exceptions, for they require pointers access the memory.
Mathematical Operations in Programming
Arithmetic operations are among the most basic operations that computers can perform. In fact, one of the components of the processor is called Arithmetic Logic Unit (ALU). In a metaphor for the human body, the ALU would correspond to the machine's brain. If the term arithmetic is part of the brain, it sounds fair to suppose it is important for programming.
Basic Operations
Computer can perform every basic arithmetic operation: additions, subtractions, multiplications and divisions. Programming languages also provide operators or subroutines (functions or procedures) for power and rooting of numbers.
| Operation | Usual Operator |
|---|---|
| Addition | + |
| Subtraction | - |
| Multiplication | * |
| Division | / |
The division requires attentions. It is not only because the divisor must not be zero, but also because there are two kinds:
- Real division: division on which at least one of the operands is a real number. The real division results in a real number, with approximate value (if the result is not exact). For instance, .
- Integer division: division on which both operands are integer numbers.
The integer division always results in an integer number.
If the division is not exact, it has a remainder.
Programming languages commonly define a special operator to get the remainder of an integer division.
Usual operators include
%ormod. For instance, (integer part); (remainder; 5 divided by 2 has 1 as remainder).
There exists programming languages that provide two operators for division: one for real division (such as /), another for integer division (such as \ or //).
In programming languages that provide a single operator for division, the usual convention is that the division of two integer numbers in an integer division.
Any division in which at least one of the operands is a real number is a real division.
Thus, it is important to write numbers such as 2.0 to ensure real divisions.
Another benefit is that the use of an explicit .0 makes it easier to explain the intention of performing a real division to other people who read the source code.
Advanced Operations
Besides basic operations, programming languages typically provide resources for trigonometry, probability and statistics. Some programming languages also provide resources for, for instance, algebra, geometry and topology.
Besides pure Mathematics, operations can be used for applied Math. For instance, it is possible to create simulations, physics calculus and processing, and graphical modelling (with resources such as matrices).
The Retirement of the Calculator and Spreadsheets
Computers are much more powerful, capable and flexible machines than calculators. After learning the basics of a programming language, traditional calculators can be retired. After learning some more, it is possible to retire spreadsheet programs, such as LibreOffice Calc and Microsoft Word.
Most programming languages enable to do everything that calculators and spreadsheets can do, without the limitations imposed by the previous technologies. In other words, a programming language turns computers into tools for Mathematics.
Similarly to programming languages, you will be able to choose the best tool to solve problems. For simple problems, perhaps it is a calculator. For more complex problems, it may be a spreadsheet. For any of the previous problems and even more complex problems, a computer may become a better option.
Digital Arithmetic
Daily mathematics commonly use decimal numbers, that is, numbers in base 10. Digital mathematics use binary numbers, that is, numbers in base 2.
All values processed by a computer are encoded as sequences of binary digits.
The following subsections briefly comment about numeric codification for computers. The programming languages do the conversion automatically; thus, the content is illustrative, to help you to understand a bit more about how computers work.
Integer Number Arithmetic
In Data Types, it was commented about the choice of integer numbers for operations that require precision. At this moment, it is worth to understand more about them.
The codification of natural numbers in digital systems is immediate, for it can be represented as sums of base 2 powers. A sequence of bits can encode different natural values. By default, the sequence starts from zero, as that is the value of the first natural number. The values comprehend the interval ranging from to , that is, .
Therefore, if 4 bits are used to encode numbers with 4 bits, it is possible to write numbers between and (). The following table lists every possible values with 4 bits binary representation. To understand the third row of the table, it is simpler to visualize the binary representation with zeros padding the left side of the number, to complete the 4 bits.
| Decimal | Binary | Binary (4 bits) |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 10 | 0010 |
| 3 | 11 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | 1000 |
| 9 | 1001 | 1001 |
| 10 | 1100 | 1100 |
| 11 | 1101 | 1101 |
| 12 | 1100 | 1100 |
| 13 | 1101 | 1101 |
| 14 | 1110 | 1110 |
| 15 | 1111 | 1111 |
The value 16 would require an additional bit, as presented in the following table. The inclusion of the additional bit allows writing numbers from 0 to 31, effectively doubling the total of possible values.
| Decimal | Binary | Binary (5 bits) |
|---|---|---|
| 0 | 0 | 00000 |
| 1 | 1 | 00001 |
| 2 | 10 | 00010 |
| 3 | 11 | 00011 |
| 4 | 100 | 00100 |
| 5 | 101 | 00101 |
| 6 | 110 | 00110 |
| 7 | 111 | 00111 |
| 8 | 1000 | 01000 |
| 9 | 1001 | 01001 |
| 10 | 1100 | 01100 |
| 11 | 1101 | 01101 |
| 12 | 1100 | 01100 |
| 13 | 1101 | 01101 |
| 14 | 1110 | 01110 |
| 15 | 1111 | 01111 |
| 16 | 10000 | 10000 |
| 31 | 11111 | 11111 |
To convert a value from binary to decimal, each digit of the binary number is multiplied by a corresponding power of 2, and all values are added. The calculus start from the least significant digit (the right-most one) with a multiplication by the power of , until the least significant digit (the left-most one) by the power of , with representing the number of bits considered.
| Decimal | Binary | Calculus to Convert From Binary to Decimal |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 10 | |
| 3 | 11 | |
| 4 | 100 | |
| 5 | 101 | |
| 6 | 110 | |
| 7 | 111 | |
| 8 | 1000 | |
| 9 | 1001 | |
| 10 | 1100 | |
| 11 | 1101 | |
| 12 | 1100 | |
| 13 | 1101 | |
| 14 | 1110 | |
| 15 | 1111 | |
| 16 | 10000 | |
| 31 | 11111 |
Natural numbers in programming are usually named unsigned integer. The term is used because the codification of an integer number (which can also be negative) requires choices to encode the sign. Numbers that are signed integers or, simply, integer numbers must represent the sign. There are two commons choices to encode integer numbers:
- Use a sign bit;
- Use two's complement.
Programming languages normally represent integer numbers in two's complement. The use of two's complement allows performing subtractions by means of sums and to represent an additional value for a given quantity of bits.
For instance, for 8 bits (1 byte) integers, the following table relates the binary representation with encoded values for natural number (unsigned int), signed integer using a sign bit, and signed integer using two's complement. It is interesting to note that a same binary representation can have multiple interpretations. The interpretation for the meaning depends on the chosen encoding and decoding.
| Binary representation | Unsigned integer | Signed integer (sign bit) | Signed integer (two's complement) |
|---|---|---|---|
| 00000000 | 0 | 0 | 0 |
| 00000001 | 1 | 1 | 1 |
| 00000010 | 2 | 2 | 2 |
| 01111111 | 127 | 127 | 127 |
| 10000000 | 128 | -0 | -128 |
| 10000001 | 129 | -1 | -127 |
| 10000010 | 130 | -2 | -126 |
| 11111110 | 254 | -126 | -2 |
| 11111111 | 255 | -127 | -1 |
For practical programming activities, it is important to know the existence of encoding because there are two usual approaches to represent the precision of integer numbers (that may vary among languages):
- Fixed precision integer number, that depends on a fixed number of bits for encoding;
- Arbitrary precision integer number, that allows a varying number of bits for encoding.
In the case of fixed precision, there is a maximum and a minimum value for each number of bits used for representation. For instance, with one byte (8 bits), it is possible to represent 256 numbers (0 to 255 without signal; -128 to 127 in two's complement). The greater the number of bits or bytes used for codification, the greater will be the interval of numbers that can be represented. The following table presents a summary of commonly used amount of bytes used for integer numbers in programming languages. The minimum value for unsigned integers is always zero.
| Number of bits | Number of bytes | Maximum integer (signed) | Minimum integer (two's complement) | Maximum integer (two's complement) |
|---|---|---|---|---|
| 1 | - | 1 | -1 | 0 |
| 8 | 1 | 255 | -128 | 127 |
| 16 | 2 | 65535 | -32768 | 32767 |
| 32 | 4 | 4294967295 | -2147483648 | 2147483647 |
| 64 | 8 | 18446744073709551615 | -9223372036854775808 | 9223372036854775807 |
The maximum and minimum values for 8, 16 and 32 bits (1, 2 and 4 bytes, respectively) are common in digital games. For instance, if you have ever played a Role-Playing Game (RPG) on which the attributes vary from 0 to 255, or from -128 to 127, the reason is that the values are stored in a variable of the type integer with the size of one byte.
The previous table helps to decide about the type and size of integer number that should be used depending on the expected values for an integer type variable. The choice is important because sums (or products) that exceed the maximum value result in an incorrect result called overflow. Similarly, differences (or multiplications) that exceed the minimum value result in an incorrect result called underflow. In some languages, such as Portuguese, the errors are also called bit burst, because the result would require an amount of bits for representation that is greater than the available one. In the lack of an additional bit, the error manifest itself in the sign bit.
Overflow and underflow happen because, both in sign bit and in two's complement, the most significant bit is used as the sign. If an operation change the value of the most significant bit, the sign of the result will be reversed.
A simple way to verify for an occurrence of overflow consists in comparing signs. If two positive values are added (or multiplied) and the result is negative, it can be inferred that the result is incorrect and that overflow happened. Analogously, if two negative values are added and the result is positive, it can be inferred that the result is incorrect and that an underflow happened.
This works because the sum or multiplication of two positive number should also be a positive number. Similarly, the sum of two negative values must also result in a negative value, as well as the multiplication of a positive by a negative number (or vice-versa).
In programming languages that adopt integer numbers with 4 bytes, the occurrence of overflow and underflow is possible and probably, depending on the values that will be used. In programming languages that adopt integer numbers with 8 bytes, the occurrence of overflow and underflow is improbably, except if the program uses very large or small numbers. However, improbably is not impossible; it exists and requires attention to avoid errors.
Some program languages provide integer numbers with arbitrary precision, using arbitrary-precision arithmetic (also called big number or bignum arithmetic). In arbitrary-precision arithmetic, the number of bits used for codification is variable. Thus, in practice, the limitation of values that can be stored depends only on the quantity of free memory available in the system.
Real Number Arithmetic
The real number arithmetic traditionally used in computers is called floating-point arithmetic. As the representation of floating-point numbers is slightly more complex than the one for integer numbers, the remainder of the subsection focus in more practical issues.
The first point that requires attentions is the fact that is not always possible to represent the decimal part of real numbers with precision using binary numbers. This is not only restricted to irrational numbers or periodic cycles, but also for any number that cannot be written as a sum of powers of negative exponents of 2.
While the integer part is composed by sums of powers of 2 (), the decimal part is composed by sums of the inverse of the division of powers of two ( = ). This means that numbers such as or () can be written with their exactly in binary representation. On the other hand, the number cannot, because it can only be approximate (). To obtain the terms, new values that do not exceed the adopted value (, in this case) are summed, while the other values are ignored. The higher the number of values used for the approximation, the betters will the precision; however, the value will never be exact.
The second point that requires attention refers to the limited precision of floating-point arithmetic. This means that any calculus using floating-point numbers is susceptible to potential rounding errors (or even incorrect values).
Although the margin of error can be small (and, potentially, negligible) in some cases, successive operations using approximated values are subject to accumulated errors. In other words, errors that could be negligible at the start can become more and more significant.
Thus, when precision is fundamental for a problem, it can be better to use integer numbers instead of floating-point numbers. Another option is using alternative codifications for real numbers. One example of alternative codification is called binary-coded decimal (BCD), that is used for financial and industrial calculus. BCD is less efficient than floating-point regarding the use of memory and processor, though it is more precise (because it encodes each digit of a number individually).
Operators' Precedence
As it happens in Mathematics, operators in programming can also have different priority when evaluated in expressions. As in Mathematics, it is usually also possible to modify the order evaluation using parentheses. Expressions with parentheses have the highest priority for evaluation.
In general, in decreasing order of precedence:
- Grouping: expressions surrounded by parentheses (
()) have the highest priority for evaluation; - Subroutine call (function, procedure, method), exponential;
- Multiplication, division and remainder;
- Addition, subtraction;
- Assignment.
In the previous list, items that appear before are evaluated before the ones that appear after them. This means that an expression such as:
x = 1 - 2 * 3 / 4.0
Results in -0.5, because is calculated as:
x = 1 - ((2 * 3) / 4.0)
It is worth remembering that, in the example, the equal (=) is an assignment, not an equality.
The evaluation matches the daily Math evaluation, for the expression corresponds to:
In the equation, the equal means equality, not assignment.
Solving the expression step by step (as a computer):
Personally, I prefer to use parentheses even in situations in which they are not necessary, because they make it easier to read expressions. It is much easier to identify operations that occur first in the example with parentheses than in the one without them.
Mathematics in Programming
As usual, the theoretic introduction is more complex than the use of arithmetic in programming. The next sections provide some examples of how to use Math expressions in practice.
Flowcharts: Flowgorithm
In Flowgorithm, the operators used for arithmetic are:
- Addition:
+; - Subtraction:
-; - Multiplication:
*; - Division:
/; - Remainder of division:
%ormod; - Power:
^.
More details can be found in the documentation.
To calculate square roots, it is possible to use sqrt().

The following block provides a transcription of the code in the image.
Main
Integer addition
addition = 1 + 2
Output addition
Integer subtraction
subtraction = 1 - 2
Output subtraction
Integer multiplication
multiplication = 1 * 3
Output multiplication
Integer integerDivision
integerDivision = 9 / 4
Output integerDivision
Integer intergerDivisionRemainder
intergerDivisionRemainder = 9 % 4
Output intergerDivisionRemainder
Real divisionReal
divisionReal = 9 / 4
Output divisionReal
Integer power
power = 10 ^ 5
Output power
Real squareRoot
squareRoot = sqrt(9)
Output squareRoot
Real cubeRoot
cubeRoot = 1000 ^ (1.0 / 3.0)
Output cubeRoot
Real x
x = 1 - ((2 * 3) / 4.0)
Output x
EndTo store a result, an Assign block can be used.
The choice of the type for the result is based according to the type of the variable that will store the result. If the variable is real, the result will also be real. Thus, to perform an integer division, a variable of the type integer must be used.
Visual Programming Language: Scratch
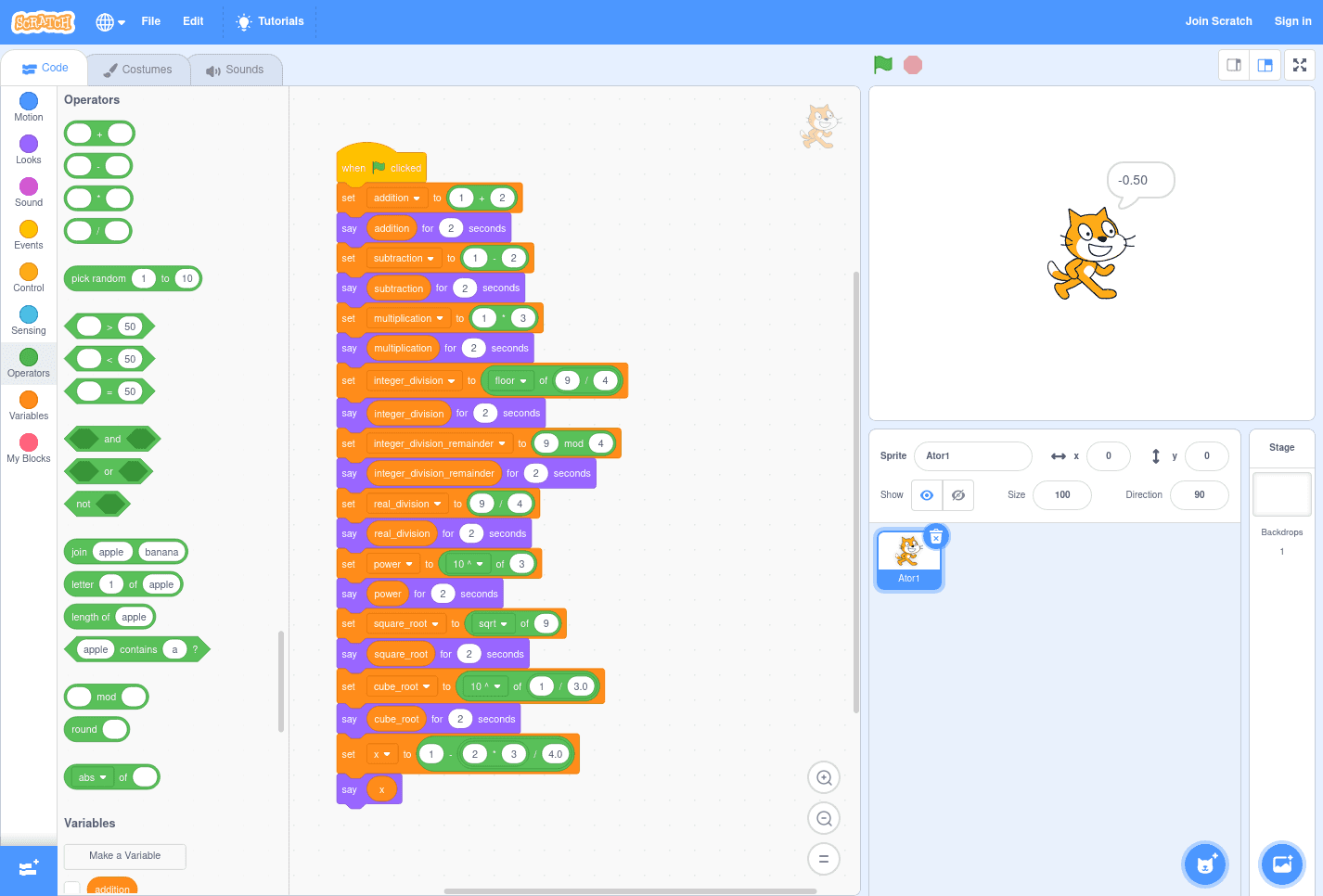
In Scratch, mathematics operators and functions are available in Operators.
For basic arithmetic operators, each operation is represented by their symbol (+, -, *, /).
For the division remainder, there is the _ mod _ block.
For other operations, the abs of _ block should be used, replacing abs with:
- For power: 10 ^
_(for base 10) or e ^_(for the base using the Euler's number -- approximately 2.71828182); - For square root: sqrt;
- To round down values for integer division: floor of
_.
A limitation the standard blocks is the lack of support for powers with bases different from 10 or . To simplify the example, the program in Scratch performs a calculation for the cube root different from the others in this page ( instead of ).
With a bit of more advanced Math, it is possible to calculate values for other bases. For non-negative bases, an alternative is to use properties of logarithms to change bases. For the provided bases, it is possible to use a logarithm with base 10 for powers of 10:
Or the natural logarithm (or Napierian) for powers of :
Most programming languages provide commands or functions to calculate powers; thus the example is merely illustrative.
Textual Programming Languages: JavaScript, Python, Lua e GDScript
Before starting to calculate Math expressions in programming language, it is worth to refer to the documentation about operator precedence.
- JavaScript: documentation;
- Python: documentation;
- Lua: documentation;
- GDScript: documentation.
Basic Arithmetic Operations
The following source code blocks provide examples of addition, subtraction, multiplication, integer division, integer division remainder, real division, power and rooting in JavaScript, Python, Lua and GDScript. Next, they define the example of an expression using parentheses as defined previously in the text. Finally, they provide a last example with the use of variables as operands of an arithmetic operation.
let addition = 1 + 2
console.log(addition)
let subtraction = 1 - 2
console.log(subtraction)
let multiplication = 1 * 3
console.log(multiplication)
let integer_division = Math.floor(9 / 4)
console.log(integer_division)
let integer_division_remainder = 9 % 4
console.log(integer_division_remainder)
let real_division = 9 / 4
console.log(real_division)
let power = Math.pow(10, 5)
console.log(power)
// In modern browsers:
power = 10 ** 5
console.log(power)
let square_root = Math.sqrt(9)
console.log(square_root)
let cube_root = Math.pow(1000, 1.0 / 3.0)
console.log(cube_root)
// Example of expression.
let x = 1 - ((2 * 3) / 4.0)
console.log(x)
x = x + x
console.log(x)addition = 1 + 2
print(addition)
subtraction = 1 - 2
print(subtraction)
multiplication = 1 * 3
print(multiplication)
integer_division = 9 // 4
print(integer_division)
integer_division_remainder = 9 % 4
print(integer_division_remainder)
real_division = 9 / 4
print(real_division)
power = 10 ** 5
print(power)
import math
square_root = math.sqrt(9)
print(square_root)
cube_root = 1000 ** (1.0 / 3.0)
print(cube_root)
# Example of expression.
x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)local addition = 1 + 2
print(addition)
local subtraction = 1 - 2
print(subtraction)
local multiplication = 1 * 3
print(multiplication)
local integer_division = 9 // 4 -- Requires Lua 5.3 or more up-to-date.
print(integer_division)
integer_division = math.floor(9 / 4) -- Alternative for previous versions.
print(integer_division)
local integer_division_remainder = 9 % 4
print(integer_division_remainder)
local real_division = 9 / 4
print(real_division)
local power = 10 ^ 5
print(power)
local square_root = math.sqrt(9)
print(square_root)
local cube_root = 1000 ^ (1.0 / 3.0)
print(cube_root)
-- Example of expression.
local x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)extends Node
func _ready():
var addition = 1 + 2
print(addition)
var subtraction = 1 - 2
print(subtraction)
var multiplication = 1 * 3
print(multiplication)
var integer_division = 9 / 4
print(integer_division)
var integer_division_remainder = 9 % 4
print(integer_division_remainder)
var real_division = 9 / 4.0
print(real_division)
var power = pow(10, 5)
print(power)
var square_root = sqrt(9)
print(square_root)
var cube_root = pow(1000, (1.0 / 3.0))
print(cube_root)
# Example of expression.
var x = 1 - ((2 * 3) / 4.0)
print(x)
x = x + x
print(x)From the previous languages, GDScript distinguishes integer divisions from real division based on the type of operands.
Thus, a real division is performed with 9 / 4.0 instead of 9 / 4.
The previous Math operations are often used in programming. In particular, the use of variables to store intermediate results is common. With good names for variables, it is possible to assist reading and understanding the code.
Increment, Decrement and Assignment Operations
For convenience, there exists programming languages that provide a combination of the assignment operators with an arithmetic operator. The main ones usually are:
+=,-=,*=,/=, and%=:x += 1corresponds tox = x + 1;x -= 2corresponds tox = x - 2;x *= 3corresponds tox = x * 3;x /= 4corresponds tox = x / 4.
The previous operators usually work with any numeric type. In some programming languages, the operator
+=used with strings performs a concatenation.++and--: increment or decrement by a unit (usually only for integer values). For instance:- Pre-increment:
++x; - Post-increment:
x++; - Pre-decrement:
--x; - Post-decrement:
x--.
The difference between pre and post is the ordem in which the operation is performed and the reuslt is returned. In pre operations, the operation is performed before returning the value. For instance, in JavaScript:
x = 0 y = ++x console.log(x, y) // x = 1, y = 1In post operations, the result is returned before the calculus of the operation. For another example using JavaScript:
x = 0 y = x++ console.log(x, y) // x = 1, y = 0Many times, the operation is used in a line of code by itself, with the result ignored. In this case, the usage is indifferent. Some compilers or interpreters can generate different code for the two operators, though, many times, the optimization performed by the tool generate equivalent code.
- Pre-increment:
The operators ++ and -- are not provided by every programming language.
For instance, Python e GDScript do not define any of them.
The workaround is simple: it suffices to use += 1 and -= 1, respectively.
Likewise, there are programming languages (such as Lua) that do not provide any of the previous operators.
Thus, every operation must be performed explicitly; for instance, x = x + 1.
let i = 0
console.log(i)
++i // i = i + 1
console.log(i)
i++ // i = i + 1
console.log(i)
i += 1 // i = i + 1
console.log(i)
i -= 2 // i = i - 2
console.log(i)
i *= 3 // i = i * 3
console.log(i)
i /= 4.0 // i = i / 4.0
console.log(i)i = 0
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i -= 2 # i = i - 2
print(i)
i *= 3 # i = i * 3
print(i)
i /= 4.0 # i = i / 4.0
print(i)local i = 0
print(i)
i = i + 1
print(i)
i = i + 1
print(i)
i = i + 1
print(i)
i = i - 2
print(i)
i = i * 3
print(i)
i = i / 4.0
print(i)extends Node
func _ready():
var i = 0
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i += 1 # i = i + 1
print(i)
i -= 2 # i = i - 2
print(i)
i *= 3 # i = i * 3
print(i)
i /= 4.0 # i = i / 4.0
print(i)Programming features like the previous are, at times, called syntactic sugar. They are conveniences provided by the language to make common programming activities faster.
Smallest and Largest Integer Values
Python 3 is a language that provides arbitrary-precision integer numbers.
However, Python 2 does not.
In Python 2, the maximum integer value can be determined with sys.maxsize (requires import sys).
The minimum one can be found with -sys.maxsize - 1.
JavaScript and Lua have limits for integer numbers (that are encoded as real numbers internally).
In JavaScript, it is possible to refer to the maximum value with Number.MAX_SAFE_INTEGER.
The minimum value can be found using Number.MIN_SAFE_INTEGER.
In Lua, the maximum integer value is provided by math.maxinteger; the smallest integer value can be accessed with math.mininteger.
In GDScript, integer numbers are encoded as signed 64-bit integers.
let int_min = Number.MIN_SAFE_INTEGER
let int_max = Number.MAX_SAFE_INTEGER
console.log(int_min)
console.log(int_max)import sys
int_min = -sys.maxsize - 1
int_max = sys.maxsite
print(int_min)
print(int_max)local int_min = math.mininteger
local int_max = math.maxinteger
print(int_min)
print(int_max)extends Node
func _ready():
# O valor -9223372036854775808 não pode ser atribuído diretamente.
var int_min = -9223372036854775807 - 1
var int_max = 9223372036854775807
print(int_min)
print(int_max)Examples
With the previous arithmetic operations, it is already possible to solve many daily problems using programming. It is also possible to solve many Math and Physics problems from high school and college.
Uniformly Varied (Accelerated) Rectilinear Movement (Motion)
It is not necessary to be a Physics expert to implement existing equations. It suffices to observe symbols and operators, then define variables for the symbols and write expressions combining variables with operators from the chosen programming language.
Velocity as Function of Time
With:
- and in m/s (meters per second);
- in m/s²;
- in s. Technically, it is a time interval (or difference, that is, would be a more suitable representation).
You can choose any name that you wish for the variables.
For instance, they could be called vf, v0, a and t, for code that resembles the equation.
If you do not want to remember what each symbol means in the future, they could have names such as initial_velocity, acceleration, time and final_velocity.
Any programming language can be used for implementation.
As all values can be real numbers, the most suitable type for the variables is real.
In particular, the choice of integer types could lead to incorrect values if the result of the division was not an integer number.
For instance, a result such as 1.5 should correspond to 1.5 m/s, though the obtained result would be 1 m/s.
In the following examples, the value provided for the variables are arbitrary. You can change them as you wish.
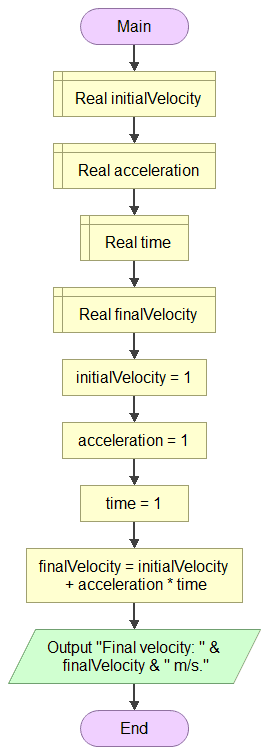
Main
Real initialVelocity
Real acceleration
Real time
Real finalVelocity
initialVelocity = 1
acceleration = 1
time = 1
finalVelocity = initialVelocity + acceleration * time
Output "Final velocity: " & finalVelocity & " m/s."
End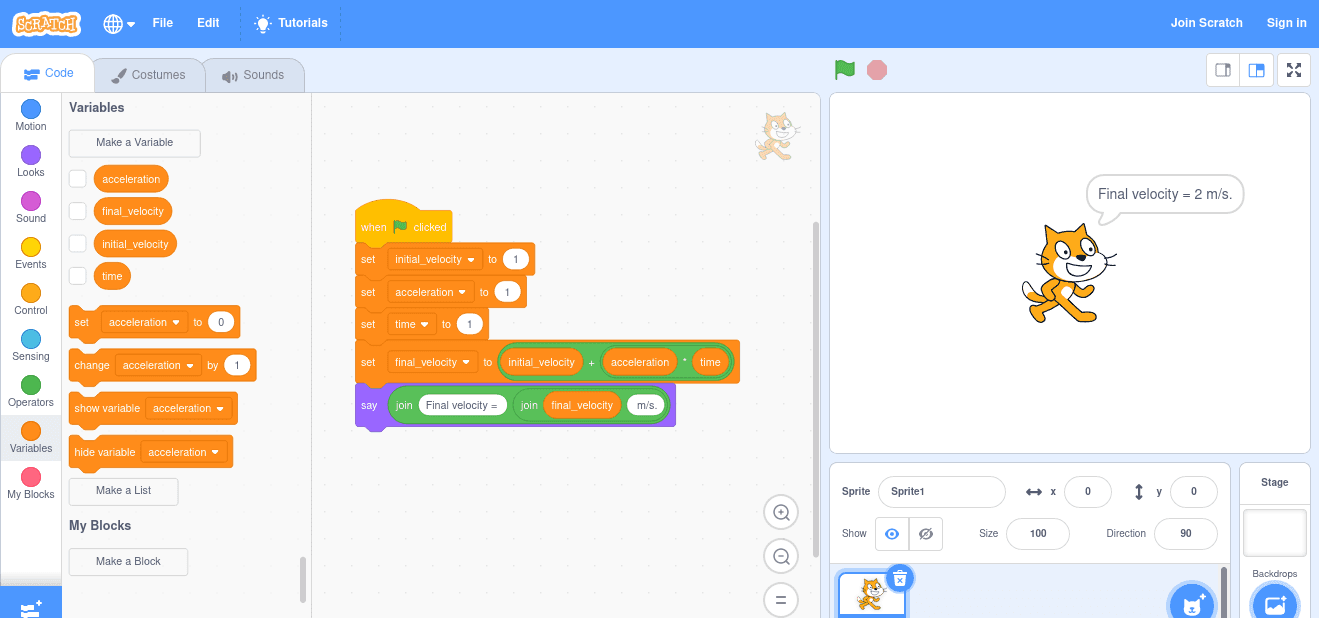
let initial_velocity = 1
let acceleration = 1
let time = 1
let final_velocity = initial_velocity + acceleration * time
console.log("Final velocity = ", final_velocity, " m/s.")initial_velocity = 1
acceleration = 1
time = 1
final_velocity = initial_velocity + acceleration * time
print("Final velocity = ", final_velocity, " m/s.")local initial_velocity = 1
local acceleration = 1
local time = 1
local final_velocity = initial_velocity + acceleration * time
print("Final velocity = ", final_velocity, " m/s.")extends Node
func _ready():
var initial_velocity = 1
var acceleration = 1
var time = 1
var final_velocity = initial_velocity + acceleration * time
print("Final velocity = ", final_velocity, " m/s.")Personally, I would recommend to documentate the expected units for the calculus in the srouce code. In this case, as the equation and the units are close in the code, it would be unnecessary. However, in more complex programs, it can be convenient to provide documentation for the parameters in the source code.
You can add comments about the expected units for each variable. For instance, in the JavaScript code:
// In m/s.
let initial_velocity = 1
// In m/s².
let acceleration = 1
// In s.
let time = 1
// Calculus of the velocity as function of time.
// In m/s.
let final_velocity = initial_velocity + acceleration * time
console.log("Final velocity = ", final_velocity, " m/s.")Another possibility is including the unities to the names of the variables:
let initial_velocity_m_s = 1
let acceleration_m_s2 = 1
let time_s = 1
// Calculus of the velocity as function of time.
let final_velocity_m_s = initial_velocity_m_s + acceleration_m_s2 * time_s
console.log("Final velocity = ", final_velocity_m_s, " m/s.")Both ways make it easier understand the source code. If you (or someone else) need to modify it in the future, it would not be necessary to reread the source code to infer how it works nor the expeted units for the correct use of the program.
Besides, it is possible to read the parameters (for instance, using console input), instead of fixing them in the source code. To adapt the source code, you can use the concepts studies in Console (Terminal) Input. For instance:
let initial_velocity_m_s = parseFloat(prompt("Initial velocity (m/s):"))
let acceleration_m_s2 = parseFloat(prompt("Acceleration (m/s²):"))
let time_s = parseFloat(prompt("Time (s):"))
// Calculus of the velocity as function of time.
let final_velocity_m_s = initial_velocity_m_s + acceleration_m_s2 * time_s
console.log("Final velocity = ", final_velocity_m_s, " m/s.")
alert("Final velocity = " + final_velocity_m_s + " m/s.")initial_velocity_m_s = float(input("Initial velocity (m/s): "))
acceleration_m_s2 = float(input("Acceleration (m/s²): "))
time_s = float(input("Time (s): "))
# Calculus of the velocity as function of time.
final_velocity_m_s = initial_velocity_m_s + acceleration_m_s2 * time_s
print("Final velocity = ", final_velocity_m_s, " m/s.")print("Initial velocity (m/s):")
local initial_velocity_m_s = io.read("*number")
print("Acceleration (m/s²):")
local acceleration_m_s2 = io.read("*number")
print("Time (s): ")
local time_s = io.read("*number")
-- Calculus of the velocity as function of time.
final_velocity_m_s = initial_velocity_m_s + acceleration_m_s2 * time_s
print("Final velocity = ", final_velocity_m_s, " m/s.")With the inclusion of input, the program can calculate the velocity as function of time of the uniformly varied rectilinear movement for any values of initial velocity, acceleration and time. However, as there is no input validation, it would be possible to provide incorrect values to the program, which would lead to incorrect results.
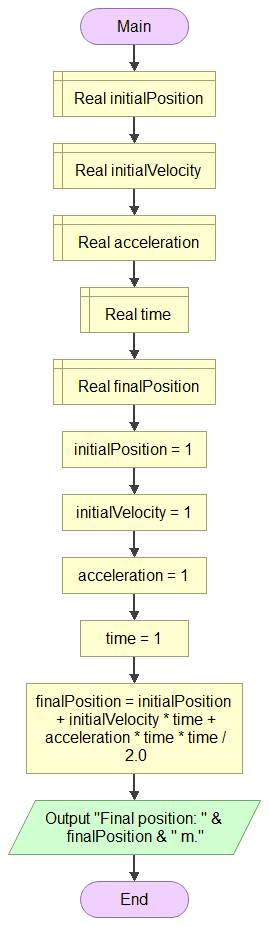
Position as Function of Time
As :
With:
- , and em m;
- in m/s;
- in s;
- in m/s².
It is important to notice that the result of the division must be a read number. Therefore, it must be ensured that the performed division is a real division instead of integer one. Otherwise, decimal results will be incorrectly rounded down.
Main
Real initialPosition
Real initialVelocity
Real acceleration
Real time
Real finalPosition
initialPosition = 1
initialVelocity = 1
acceleration = 1
time = 1
finalPosition = initialPosition + initialVelocity * time + acceleration * time * time / 2.0
Output "Final position: " & finalPosition & " m."
End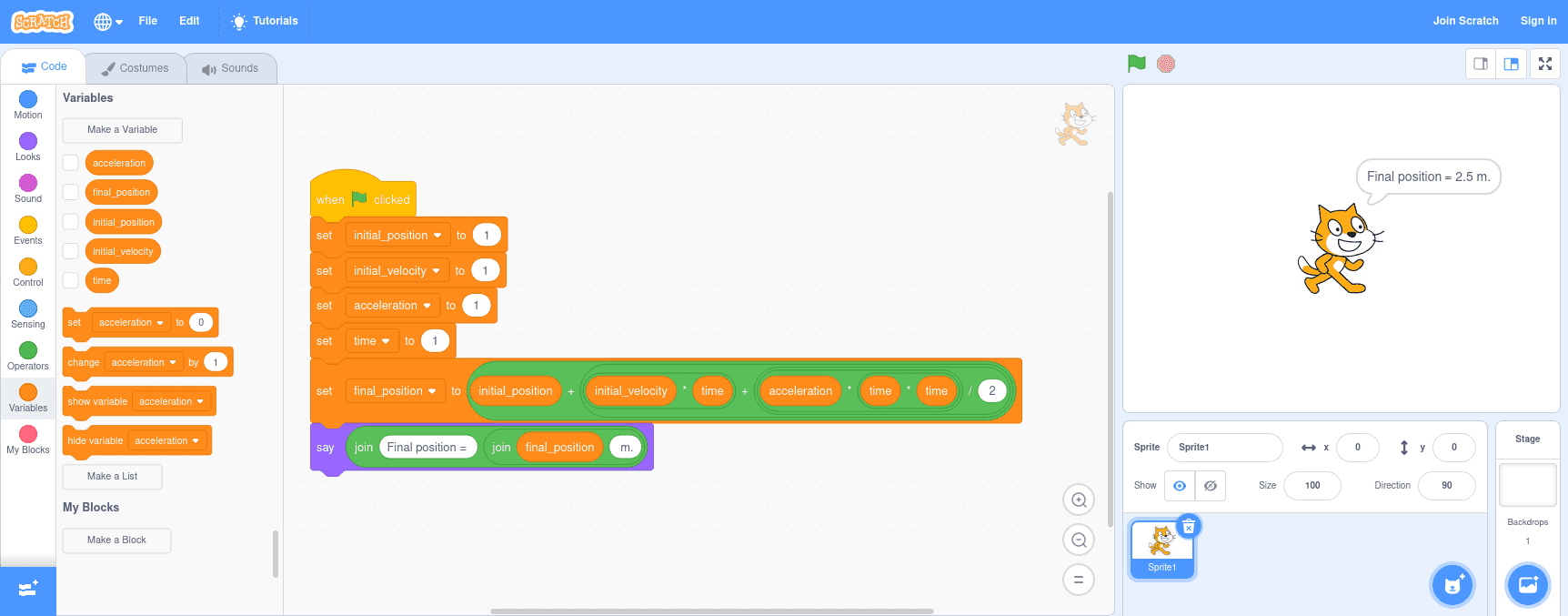
let initial_position = 1
let initial_velocity = 1
let acceleration = 1
let time = 1
let final_position = initial_position + initial_velocity * time + acceleration * time * time / 2.0
console.log("Final position = ", final_position, " m.")initial_position = 1
initial_velocity = 1
acceleration = 1
time = 1
final_position = initial_position + initial_velocity * time + acceleration * time * time / 2.0
print("Final position = ", final_position, " m.")local initial_position = 1
local initial_velocity = 1
local acceleration = 1
local time = 1
local final_position = initial_position + initial_velocity * time + acceleration * time * time / 2.0
print("Final position = ", final_position, " m.")extends Node
func _ready():
var initial_position = 1
var initial_velocity = 1
var acceleration = 1
var time = 1
var final_position = initial_position + initial_velocity * time + acceleration * time * time / 2.0
print("Final position = ", final_position, " m.")The examples calculate the square of the time using a multiplication, though it is also possible to use the power to square the number. The result would be the same.
To practice, add console input to read values for the JavaScript, Python and Lua implementations.
Calculating the Power of a Number with Logarithms
The calculus of powers using logarithms was implemented in Scratch. For further examples, it is possible to implement it in other programming languages, such as JavaScript, Python, Lua and GDScript.
To do this, some additional functions will be necessary, as they were used in the expression. In particular, the solution will require functions to calculate:
- Absolute value;
- Base 10 logarithms;
- Natural, Napierian, or base logarithms;
- A function to calculate exponential -- or simply .
To do this, it is possible to search for the constant
ein the programming language or use an approximate value, such as2.71828182.
To find the necessary functions, one can search for something like "javascript mdn logarithm" in search engines such as Google, Bing or DuckDuckGo.
- Absolute value ():
- JavaScript
Math.abs(): documentation; - Python
abs(): documentation; - Lua
math.abs(): documentation; - GDScript:
abs(): documentation.
- JavaScript
- Base 10 logarithm ():
- JavaScript
Math.log10(): documentation; - Python
math.log10(): documentation; - Lua
math.log10(): documentation; - GDScript: does not provide a predefined implementation. The calculation can use a change of base.
- JavaScript
- Base logarithm ( or ):
- JavaScript
Math.log(): documentation; - Python
math.log(): documentation; - Lua
math.log(): documentation; - GDScript:
log(): documentation.
- JavaScript
- Exponencial ():
- JavaScript
Math.exp(): documentation; - Python
math.exp(): documentation; - Lua
math.exp(): documentation; - GDScript:
exp(): documentation.
- JavaScript
With the functions, one can implement the solutions.
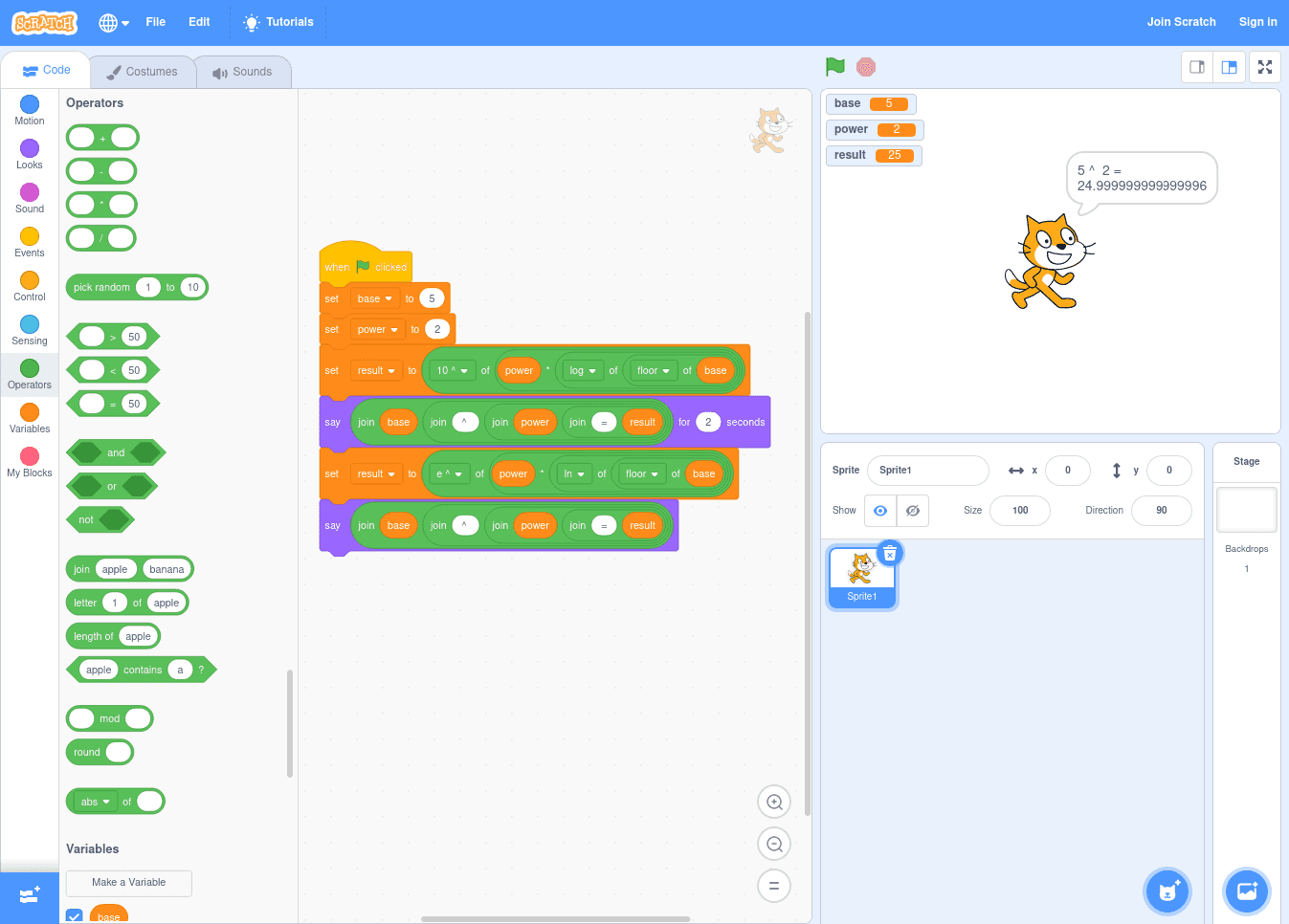
let base = 5
let power = 2
let result = Math.pow(10, power * Math.log10(Math.abs(base)))
console.log(result)import math
base = 5
power = 2
result = 10 ** (power * math.log10(abs(base)))
print(result)local base = 5
local power = 2
local result = 10 ^ (power * math.log10(math.abs(base)))
print(result)extends Node
func _ready():
var base = 5
var power = 2
var result = pow(10, power * log(abs(base)) / log(10))
print(result)GDScript is a particular case, because it does not provide a function to calculate base 10 algorithms. To solve the problem, one can perform a change of base. (). In the previous example, this was implemented as .
let base = 5
let power = 2
let result = Math.exp(power * Math.log(Math.abs(base)))
console.log(result)import math
base = 5
power = 2
result = math.exp(power * math.log(abs(base)))
print(result)local base = 5
local power = 2
local result = math.exp(power * math.log(math.abs(base)))
print(result)extends Node
func _ready():
var base = 5
var power = 2
var result = exp(power * log(abs(base)))
print(result)New Items for Your Inventory
Tools:
- Programming as a calculator;
- Programming as a spreadsheet.
Skills:
- Mathematical calculations.
Concepts:
- Integer division;
- Integer division remainder;
- Real division;
- Signed integer numbers;
- Unsigned integer numbers;
- Underflow;
- Overflow;
- Floating-point numbers;
- Accumulated error;
- Operators precedence.
Programming resources:
- Arithmetic operations.
Practice
A good source of math problems for programming is the Project Euler. However, the resource is only available in English. Furthermore, many problems require programming concepts that were not yet explained. Many require concepts such as conditional structures and loops, that will still be commented.
A simpler introduction and an alternative available in multiple (human) languages is the list of functions from Wikipedia. The simplest formulas are from elementary geometry.
To start, one of the simplest resources is the list of formulas to calculate the area of shapes. For even simple equations, refer to the list of formulas to calculate the perimeter.
There also exists a summary with a list of formulas in elementary geometry.
For convenience, the following table provides some formulas to practice.
| Shape | Area | Perimeter | Comment |
|---|---|---|---|
| Square | is the size of a side | ||
| Rectangle | is the length, é a width | ||
| Circle | is the radius | ||
| Triangle | is the base; is the height; , e are the sides | ||
| Trapezoid | and are the bases; is the height | ||
| Parallelogram | is the base; is the height; and are the sides |
| Shape | Volume | Surface area | Comment |
|---|---|---|---|
| Cube | is the size of a side | ||
| Rectangular prism | is the length; is the height; is the width | ||
| Sphere | is the radius | ||
| Circular cylinder | is the radius; is the height |
It is worth mentioning that, in the formulas, (read as pi) is a constant value (approximately 3.1415926).
Programming languages usually provide a constant for .
For instance:
- JavaScript:
Math.pi(documentation); - Python:
math.pi(documentation); - Lua:
math.pi(documentation); - GDScript:
math.pi(documentation);
Next Steps
Arithmetic operations are common in programming, even to solve non-Math problems. However, unlike school activities, the computer will perform the calculations and return the results. The role of the programmer is, thus, defining the operations that must be performed. To do this, she/he must select operators and build expressions in the correct order of operator precedence.
The advantage of solving a problem computationally is becoming able to use the same solution for other valid values. As it was done in the example with input, it is possible to solve a problem once and use the solution for other values belonging the problem's domain.
As mentioned, mathematical operations are part of the Arithmetic Logic Unit. The second part that appears in the name refer to logic and relational operations, which introduction starts in the next topic.
- Introduction;
- Entry point and program structure;
- Output (for console or terminal);
- Data types;
- Variables and constants;
- Input (for console or terminal);
- Arithmetic and basic Mathematics;
- Relational operations and comparisons;
- Logic operations and Boolean Algebra;
- Conditional (or selection) structures;
- Subroutines: functions and procedures;
- Repetition structures (or loops);
- Arrays, collections and data structures;
- Records (structs);
- Files and serialization (marshalling);
- Libraries;
- Command line input;
- Bitwise operations;
- Tests and debugging.
