Learn Programming: Relational Operations and Comparisons

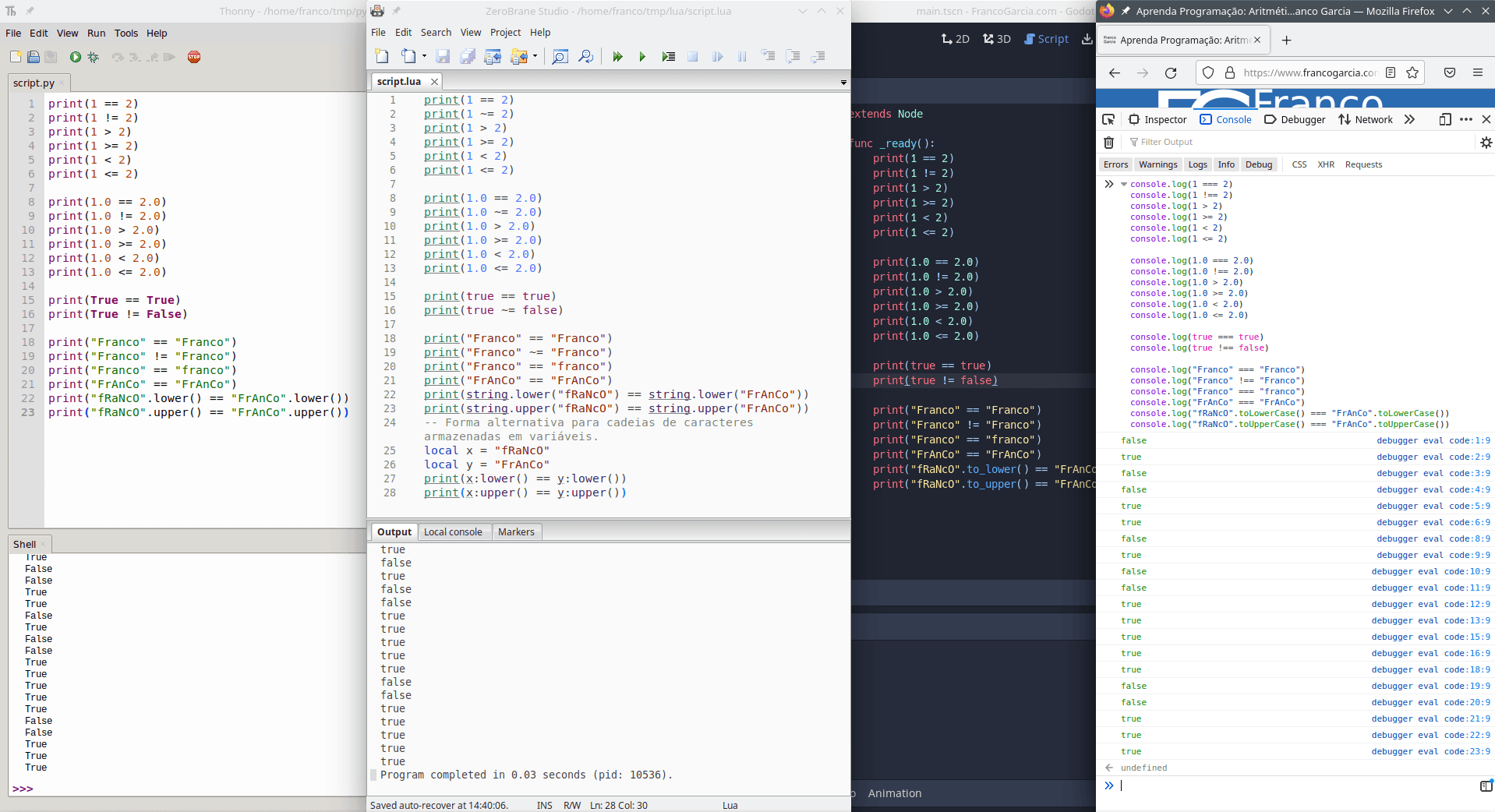
Image credits: Image created by the author using the program Spectacle.

Requirements

In the introduction to development environments, I have mentioned Python, Lua and JavaScript as good choices of programming languages for beginners. Later, I have commented about GDScript as an option for people who want to program digital games or simulations. For the introductory programming activities, you will need, at least, a development environment configured for one of the previous languages.

If you wish to try programming without configuring an environment, you can use of the online editors that I have created:

However, they do not provide all features offered by interpreters for the languages. Thus, sooner or later, you will need to set up a development environment. If you need to configure one, you can refer to the following resources.

Thus, if you have an Integrated Development Environment (IDE), or a combination of text editor and an interpreter, you are ready to start. The following example assumes that you know how to run code in your chosen language, as presented in the configuration pages.

If you want to use another language, the introduction provides links for configure development environments for the C, C++, Java, LISP, Prolog, and SQL (with SQLite) languages. In many languages, it suffices to follow the models from the experimentation section to modify syntax, commands and functions from the code blocks. C and C++ are exceptions, for they require pointers access the memory.

Comparisons

With arithmetic operations, it is possible to manipulate values. With relational operations, it is possible to compare the manipulated values.

Comparisons use operators called relational operators, for they allow relating two values to make a statement about them. In this case, the affirmation is an answer that will be a True or False logic value.

For an example, one can consider two variables that relate whether a piece of food is suitable to be eaten or if it has expired. They could be called today and expiration_day, assuming that the month and year are the same. How could one inform the computer whether the food can be eaten safely?

The answer is to compare values using a suitable relation operation to find if the answer is True (the food can be eaten) or False (the food has expired).

Relational Operations and Operators

Relation operators are binary operators (that is, that use exactly two operands), in the format x OP y, on which OP is the operator. Thus, every comparison consider two values, that must be of equivalent or compatible types.

Programming language usually provide six relational operators for value comparisons:

Equality (commonly == or =).
The operation corresponding to the Math's equality (). Programming languages that use = for assignment usually define == for equality. Programming languages that define another assignment operator (such as <- or :=) often use a single = for equality.
If x == y, then the values of x and y are equal;
Difference (commonly != or <>).
The operation corresponds to not equal in Math (). If x != y, then the values of x and y are different;
Greater than (normally >).
This operation is analogous to the Math operation with the same name (). If x > y, the value of x is greater than that of y. In other words, y is less or equal to x;
Less than (normally <).
This operation is analogous to the Math operation with the same name (). If x < y, the value of x is less than that of y. In other words, y is greater or equal to x;
Greater than or equal (normally >=).
This operation is analogous to the Math operation with the same name (). If x >= y, the value of x is either equal to that of y, or greater than it. Thus, y is less than x.
Less than or equal (commonly <=, at times =<).
This operation is analogous to the Math operation with the same name (). If x <= y, the value of x is either equal to that of y, or less than it. Thus, y is greater than x.

With some practice, it becomes intuitive to read operators in source code. Some text editors or IDEs can show the operator with the Mathematical symbol. If this suits you, it can be interesting to verify if your favorite editor or IDE provides the option.

The result of a relation operation is a logic value. For instance, 2 > 1 results True, like 2 == 2, 2 != 1, 2 != 1 and 2 >= 2. On the other hand, 2 < 1 results False, like 2 = 1, 2 <= 1 and 1 > 2.

What is the Inverse of Greater Than? What is the Inverse of Smaller Than?

It should be noted that the inverse of > is not <, but <=. If a number is not greater than the other, it can be smaller or equal to the other. This same is valid for <, which has >= as its inverse.

For instance, 1 < 2 is True. 2 > 1 is also True, as is 2 >= 1.

Thus, thinking about generic comparisons such as x > y follow the same reasoning. If x > y is False, it can be concluded either that y > x or that y = x. Any of the results is possible. To know what is the exact case, another comparison must be made.

Programming Language With Fewer Relational Operators

Some programming languages define only three relational operators: equal, less than and greater than. To obtain the other operators, results can be combined with logic operations, which will be the next topic of study (on the next page).

As an intuitive introduction, it can be stated that:

!= () corresponds to not equal;
>= () corresponds to > or =. Another possibility is thinking about greater than or equal as not less than;
<= () corresponds to < or =. Another possibility is thinking about less than or equal as not greater than.

The three main logic operators are and, or, and not. In the previous items, the use of the logic operators uses italic for emphasis.

Type Compatibility for Comparisons

To compare values of different types, they should be converted, first, to a same type. The exceptions are:

The types integer and real, that can be often compared without explicit conversions (though there exists programming languages that require an explicit conversion). When the comparison uses an implicit conversion, it is common that a good compiler will provide a warning. Some interpreters can also issue warnings;
Programming languages that use coercion for automatic type conversion.

In reality, the first case is a particularization of the second. Many programming languages consider the integer part of a real number for comparisons between real and integer numbers. The real number can be rounded down (floor), and its decimal part is truncated. Rounded down values can result in errors, as a value such as 1.99999 can become 1.0, when the expected value could be 2.0.

Personally, I prefer to explicit the conversion when it is necessary to compare an integer number with a real one, to make my intention clear. This way, it is also possible to perform the most appropriate rounding, be it down (floor), up (ceiling), or to the nearest value (round).

Value Comparisons and Reference Comparisons

In some programming languages and for some data types, there can be differences of conventions for comparisons of variables that store values and variables that store references (or memory addresses).

For instance, to compare strings in Java, the equals() method should be used instead of the operator ==. The operator compares memory addresses (x== y), while the method (x.equals(y)) compares the stored values.

Furthermore, in many programming languages, the comparison of composite types using the operator can be performed using references. In this case, one must use a suitable subroutine (function, procedure or method) to compare values, or verify it there exists custom operators, with the processing redefined by overloading them.

Definition of Custom Operators for Composite Types

Some programming languages allow specializing arithmetic, relational and/or logic operators for composite data types. This is normally called operator overloading, that is an example of polymorphism.

Although explaining and exemplifying the concept are not in the scope of this page in particular, it is important to know it because of a caveat. Not every programming language allow using predefined relational operators with composite types.

An example is the C language, that does not allow comparisons of strings using the operators = and !=, rather requiring the creation of a subroutine (function), or conditional structures and loops to perform comparisons.

Thus, before performing comparisons, it is important to check the language's documentation to learn what are the data types supported for the predefined operators.

Case Sensitivity

Comparisons of strings have another particularity. Equality and difference comparisons can distinguish between uppercase from lowercase letters, something that is called case sensitivity.

Programming languages that perform the distinction are called case-sensitive.

For instance, in a case-sensitive language:

"Franco" == "Franco" is True;
"Franco" != "Franco" is False;
"Franco" == "franco" is False.
"FrAnCo" == "FrAnCo" is True.

Thus, the comparison of each corresponding character in a string must have the same letter and the same case. To ignore the case, one possibility is converting both strings to a same case convention -- for instance, convert all characters to uppercase or all characters to lowercase.

Real Numbers Precision

Comparisons of real numbers also require attention, due to imprecision caused by the use of floating-point numbers. In general, it is not suitable to use == and != to compare floating-point numbers.

There are two alternatives:

Use <= or >=, and consider values up to the desired value;
Use a small value as an acceptable margin of error, usually called epsilon ( or ).

Some programming languages define an EPSILON constants; others do not. For instance:

JavaScript: Number.EPSILON (documentation);
Python: sys.float_info.epsilon (documentation).

In languages that do not define a constant, you can choose a value that you consider appropriate for the characteristics of your problem. Another option is to use the value defined in the C language.

C: FLT_EPSILON (for the type float), DBL_EPSILON (for the type double), LDBL_EPSILON (for the type long double) (documentation).

In my machine, the value was 2.220446049250313e-16 (), which will be used for Lua and GDScript in the following example. To illustrate the problem, one can perform a calculation such , which expected result would be . However, due to precision problem, the result will tend to be close to, though different from, zero.

let zero = 0.1 + 0.2 - 0.3
console.log(zero)
console.log(zero === 0.0) // false
console.log(Math.abs(zero) < Number.EPSILON) // true

import sys

zero = 0.1 + 0.2 - 0.3
print(zero)
print(zero == 0.0) # False
print(abs(zero) < sys.float_info.epsilon) # True

local EPSILON <const> = 2.220446049250313e-16

local zero = 0.1 + 0.2 - 0.3
print(zero)
print(zero == 0.0) -- false
print(math.abs(zero) < EPSILON) -- true

extends Node

const EPSILON = 2.220446049250313e-16

func _ready():
    var zero = 0.1 + 0.2 - 0.3
    print(zero)
    print(zero == 0.0) # false
    print(abs(zero) < EPSILON) # true

When the previous source code snippets are run, it can be observed that the comparison with 0.0 fails, although the comparison considering the EPSILON margin of error provides the correct result.

The previous example explains my recommendation from Data Types that beginners should use double instead of float in languages that provide the choice. The greater precision results into values that are close to those expected in Mathematics.

Relational Operators in Programming

It is simple to use relational operators, provided that the required care to use compatible data types and choosing a correct operator (or subroutine) to compare strings are taken.

Flowcharts: Flowgorithm

Flowgorithm allows using two of the most traditional styles of operators for equality and difference, as described in the documentation. You can choose the one you prefer; the examples will use == and != to make it easier to identify their uses in the written source code.

Equality: == or =;
Difference: != or <>;
Less than: <;
Less than or equal: <=;
Greater than: >;
Greater than or equal: >=.

Comparisons of strings are case-sensitive. However, the program does not provide predefined subroutines for case conversion. Although it is possible to create a flowchart to perform the conversion, the implementation would require resources that have not yet been described (such as loops).

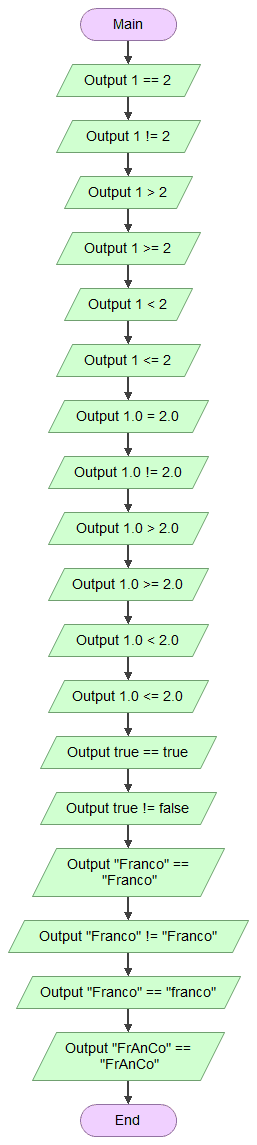
Example of relational operations in Flowgorithm: equality, difference, less than, less than or equal, greater than, greater than or qual.

The transcript of the content of the image is provided next.

Main

Output 1 == 2
Output 1 != 2
Output 1 > 2
Output 1 >= 2
Output 1 < 2
Output 1 <= 2

Output 1.0 == 2.0
Output 1.0 != 2.0
Output 1.0 > 2.0
Output 1.0 >= 2.0
Output 1.0 < 2.0
Output 1.0 <= 2.0

Output True == True
Output True != False

Output "Franco" == "Franco"
Output "Franco" != "Franco"
Output "Franco" == "franco"
Output "FrAnCo" == "FrAnCo"

End

At this time, the operators can be used in the Output or Assign blocks. In future topics, they can also be used in blocks for control flow and loops.

Visual Programming Language: Scratch

Relational operators in Scratch are available at the side menu Operators. Scratch provides only three relational operators: =, > e <. To generate the others:

!=: use a not block with the block =;
>=: use an or block. In the first position, insert a > block. In the second position, insert a = block. The order can be reversed;
<=: use an or block. In the first position, insert a < block. In the second position, insert a = block. The order can be reversed.

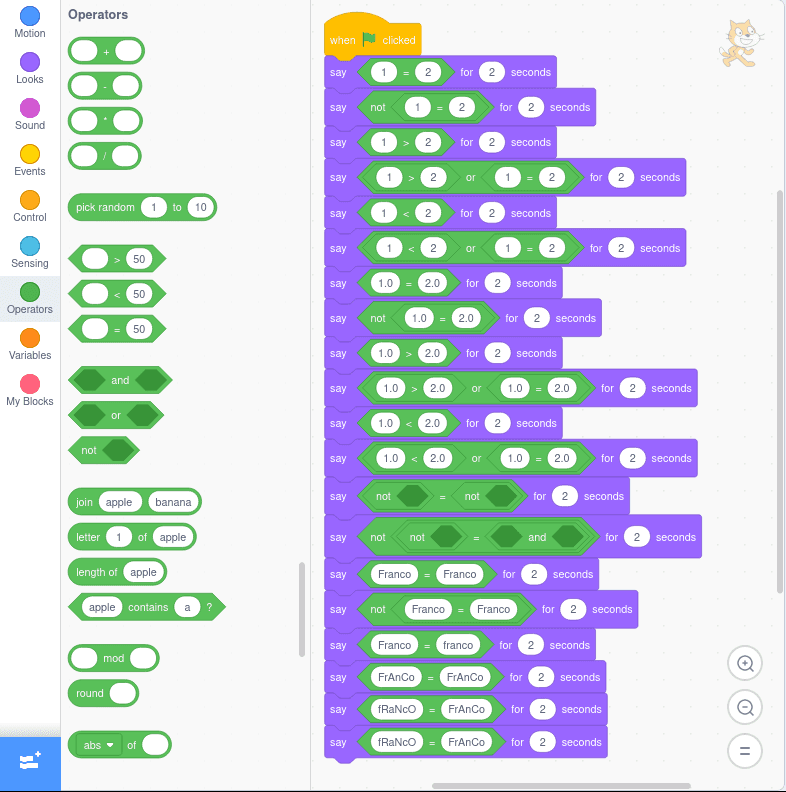
Example of relational operations in Scratch: equality, difference, less than, less than or equal, greater than, greater than or qual.

The language is not case-sensitive, that is, corresponding uppercase and lowercase letters are considered equal.

AS the languages does not provide constants for logic values, an empty not block was used as True, and an empty and block was used as False.

Textual Programming Languages: JavaScript, Python, Lua and GDScript

Except for equal and different and JavaScript, and different in Lua, the relational operators are identical in JavaScript, Python, Lua and GDScript.

Language	Equal	Different	Greater Than	Less Than	Greater Than or Equal	Less Than or Equal
JavaScript	`===`	`!==`	`>`	`<`	`>=`	`<=`
Python	`==`	`!=`	`>`	`<`	`>=`	`<=`
Lua	`==`	`~=`	`>`	`<`	`>=`	`<=`
GDScript	`==`	`!=`	`>`	`<`	`>=`	`<=`

Furthermore, the four languages allow string comparison using the equal and different operators. The four languages are case-sensitive. For conversions between uppercase and lowercase letters:

JavaScript:
- Convert to lowercase: toLowerCase() (documentation);
- Convert to uppercase: toUpperCase() (documentation).
Python:
- Convert to lowercase: lower() (documentation);
- Convert to uppercase: upper() (documentation).
Lua:
- Convert to lowercase: string.lower() (documentation);
- Convert to uppercase: string.upper (documentation).
GDScript:
- Convert to lowercase: to_lower() (documentation);
- Convert to uppercase: to_upper() (documentation).

console.log(1 === 2)
console.log(1 !== 2)
console.log(1 > 2)
console.log(1 >= 2)
console.log(1 < 2)
console.log(1 <= 2)

console.log(1.0 === 2.0)
console.log(1.0 !== 2.0)
console.log(1.0 > 2.0)
console.log(1.0 >= 2.0)
console.log(1.0 < 2.0)
console.log(1.0 <= 2.0)

console.log(true === true)
console.log(true !== false)

console.log("Franco" === "Franco")
console.log("Franco" !== "Franco")
console.log("Franco" === "franco")
console.log("FrAnCo" === "FrAnCo")
console.log("fRaNcO".toLowerCase() === "FrAnCo".toLowerCase())
console.log("fRaNcO".toUpperCase() === "FrAnCo".toUpperCase())

print(1 == 2)
print(1 != 2)
print(1 > 2)
print(1 >= 2)
print(1 < 2)
print(1 <= 2)

print(1.0 == 2.0)
print(1.0 != 2.0)
print(1.0 > 2.0)
print(1.0 >= 2.0)
print(1.0 < 2.0)
print(1.0 <= 2.0)

print(True == True)
print(True != False)

print("Franco" == "Franco")
print("Franco" != "Franco")
print("Franco" == "franco")
print("FrAnCo" == "FrAnCo")
print("fRaNcO".lower() == "FrAnCo".lower())
print("fRaNcO".upper() == "FrAnCo".upper())

print(1 == 2)
print(1 ~= 2)
print(1 > 2)
print(1 >= 2)
print(1 < 2)
print(1 <= 2)

print(1.0 == 2.0)
print(1.0 ~= 2.0)
print(1.0 > 2.0)
print(1.0 >= 2.0)
print(1.0 < 2.0)
print(1.0 <= 2.0)

print(true == true)
print(true ~= false)

print("Franco" == "Franco")
print("Franco" ~= "Franco")
print("Franco" == "franco")
print("FrAnCo" == "FrAnCo")
print(string.lower("fRaNcO") == string.lower("FrAnCo"))
print(string.upper("fRaNcO") == string.upper("FrAnCo"))
-- Alternative form for strings stored in variables.
local x = "fRaNcO"
local y = "FrAnCo"
print(x:lower() == y:lower())
print(x:upper() == y:upper())

extends Node

func _ready():
    print(1 == 2)
    print(1 != 2)
    print(1 > 2)
    print(1 >= 2)
    print(1 < 2)
    print(1 <= 2)

    print(1.0 == 2.0)
    print(1.0 != 2.0)
    print(1.0 > 2.0)
    print(1.0 >= 2.0)
    print(1.0 < 2.0)
    print(1.0 <= 2.0)

    print(true == true)
    print(true != false)

    print("Franco" == "Franco")
    print("Franco" != "Franco")
    print("Franco" == "franco")
    print("FrAnCo" == "FrAnCo")
    print("fRaNcO".to_lower() == "FrAnCo".to_lower())
    print("fRaNcO".to_upper() == "FrAnCo".to_upper())

The comparisons can be performed either using constants or variables. In Lua, it is possible to use the alternative syntax for case conversion of strings stored in variables.

It is worth remembering the required care to compare real numbers.

It should be noted that JavaScript defined the operators == e !=; however, normally it is preferable to use the versions with an extra equal sign (=== e !==). The difference is that the operator == performs implicit type conversion (using coercion), not requiring that the types are the same to return true. The same applies for difference using !=. The problem of the implicit conversion in JavaScript is that there exists many cases to consider that are not intuitive and can lead to unexpected errors (to learn more, the documentation at MDN can be referred). Thus, the operators === and !== in JavaScript are equivalent to the operators == and != of many other programming languages.

New Items for Your Inventory

Skills:

Comparisons;

Concepts:

Equality;
Difference;
Inequalities: greater than, less than, greater than or equal, less than or equal.

Programming resources:

Relational operations.

Practice

Relational operations allow relating values to define possible decisions. Although the definition of specific processing for possible scenarios depend on conditional structures, it is possible to store the values as answers and write them.

For instance, a division requires a numerator (dividend) and a denominator (divisor). The denominator must not be zero, that is, a valid division requires denominator \ne 0$$.

let denominator = 1
let valid_division = denominator !== 0
console.log("Is the denominator ", denominator, " valid in a division? ", valid_division)

denominator = 0
valid_division = denominator !== 0
console.log("Is the denominator ", denominator, " valid in a division? ", valid_division)

denominator = 1
valid_division = denominator != 0
print("Is the denominator ", denominator, " valid in a division? ", valid_division)

denominator = 0
valid_division = denominator != 0
print("Is the denominator ", denominator, " valid in a division? ", valid_division)

local denominator = 1
local valid_division = denominator ~= 0
print("Is the denominator ", denominator, " valid in a division? ", valid_division)

denominator = 0
valid_division = denominator ~= 0
print("Is the denominator ", denominator, " valid in a division? ", valid_division)

extends Node

func _ready():
    var denominator = 1
    var valid_division = denominator != 0
    print("Is the denominator ", denominator, " valid in a division? ", valid_division)

    denominator = 0
    valid_division = denominator != 0
    print("Is the denominator ", denominator, " valid in a division? ", valid_division)

Create programs that perform comparisons for the following scenarios, writing the resulting logic value as output:

The minimum age to vote in a given country is 16 years old. Could a person whose age is stored in the variable age_years vote in the country?
The minimum average for approval in a school is 6.5, based in the average of 3 values. Would a person whose grades are g1, g2 e g3 (values provided as input by a user) be approved in the school?
In the previous question, you can now consider a weighted average. g1 corresponds to 20% of the average; g2 as 35%; g3 as 45%. Would a person with the same grades provided previously be approved?
Store the value of a name. Is the chosen name Franco? Be careful with case differences. For instance, FRANCO and franco correspond to the name Franco, as does FRAnco.
What is your favorite food? What is the favorite food of your best friend? Do you have the same favorite food?
To calculate a second-degree equation in the form that admit real roots, the discriminant must not be negative. Write a program that stores values for a, b and c of a second-degree equation and answer whether the equation has real roots.
A store has a maximum allowed occupation of maximum_allowed_people_number. A total of people_number are in the store at this moment. Is the store full?
Request the input of a number. Is the number even? Even numbers are multiple of 2, that is, the remainder of the division by 2 must be zero.
Write comparisons to determine the answer to the following expressions:
- (warning: the expression requires real numbers)
Some people say that it is possible to multiply the age of a dog by 7 to estimate its "human age". Request the input of an age for a dog. Does the age of the dog corresponds to 28 human years or more?
For a more scientific estimation of the "human age" of a dog, you can refer to this page.

Next Steps

Although relation operations can seem superfluous when individually analyzed, they will become important to write choices and decision-making in programs.

Thus, if you do not yet identify practical applications that require the use of relational operations, they will become virtually indispensable for using conditional and repetition structures.

However, a careful reading of the text can generate a pertinent doubt. Relation operations use two operands. How to proceed when it is necessary to compare more than two values? Furthermore, how to combine comparisons that require the use of multiple variables, perhaps that are not even directly related?

For instance, the access to restricted page can require an e-mail address and a password. The e-mail must be valid; the combination of e-mail and password must be correct. What to do?

The answer is to combine intermediate results with logic operators. The section about Scratch provided an example of creating the operators !=, >= and <= with the operations not and or. It is convenient to formalize the use of such operators and introduce new ones to enable you to use them in your programs.

← Previous:
Learn Programming: Arithmetic and Basic Mathematics

Next:→
Learn Programming: Logic Operations and Boolean Algebra