Learn Programming: Bitwise Operations
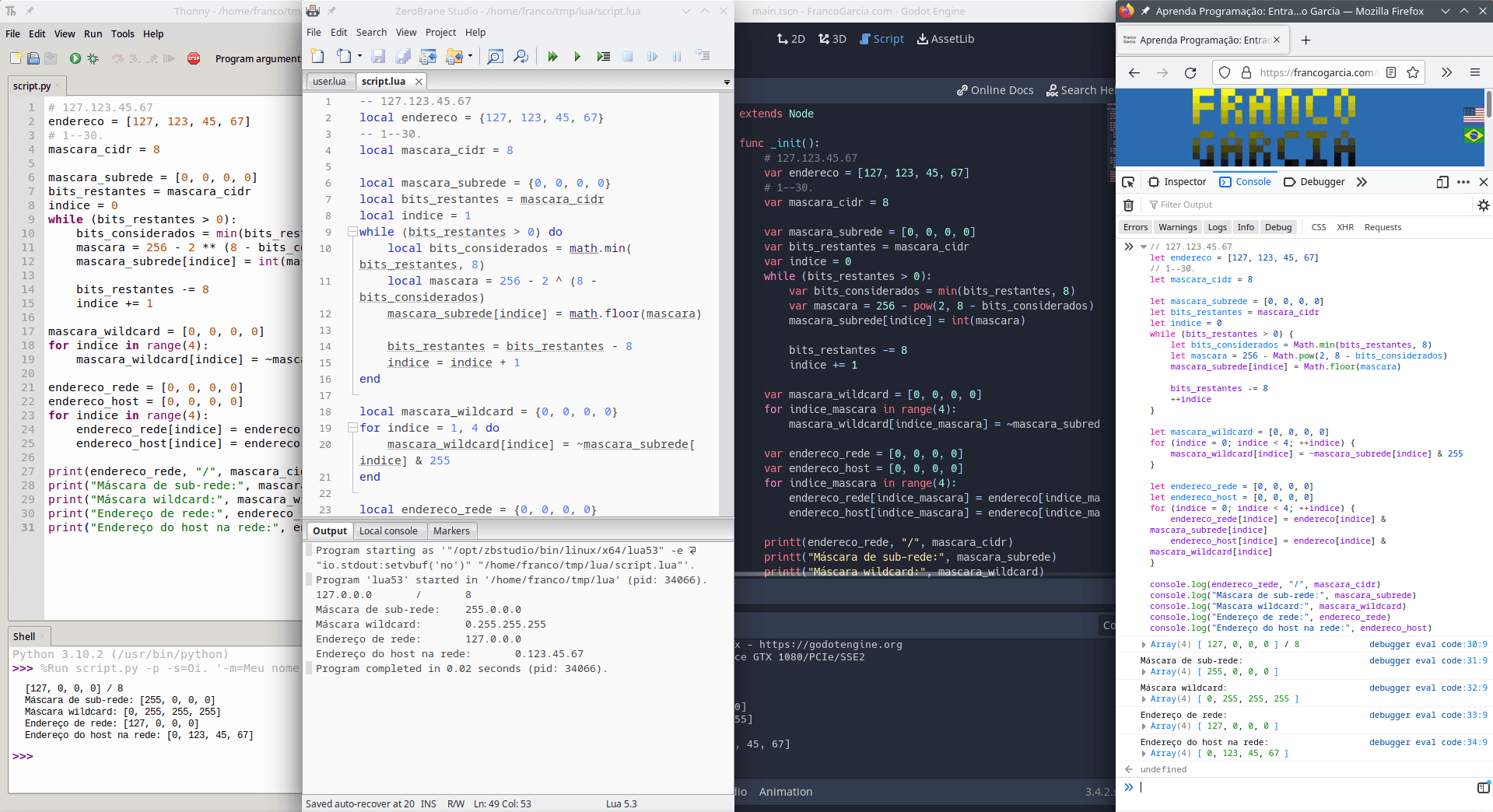
Image credits: Image created by the author using the program Spectacle.
Requirements
In the introduction to development environments, I have mentioned Python, Lua and JavaScript as good choices of programming languages for beginners. Later, I have commented about GDScript as an option for people who want to program digital games or simulations. For the introductory programming activities, you will need, at least, a development environment configured for one of the previous languages.
If you wish to try programming without configuring an environment, you can use of the online editors that I have created:
However, they do not provide all features offered by interpreters for the languages. Thus, sooner or later, you will need to set up a development environment. If you need to configure one, you can refer to the following resources.
Thus, if you have an Integrated Development Environment (IDE), or a combination of text editor and an interpreter, you are ready to start. The following example assumes that you know how to run code in your chosen language, as presented in the configuration pages.
If you want to use another language, the introduction provides links for configure development environments for the C, C++, Java, LISP, Prolog, and SQL (with SQLite) languages. In many languages, it suffices to follow the models from the experimentation section to modify syntax, commands and functions from the code blocks. C and C++ are exceptions, for they require pointers access the memory.
One Byte, Eight Bits
The logic data type represents two possible values: True or False.
One bit can represent two binary values.
Therefore, one bit would be enough to store a variable of the logic type.
However, reality is not as simple as the theory. Programming languages often define logic type variables with one byte, or even four or eight bytes. In other words, 8, 32 or 64 bits, even if 1 would be enough.
A waste that has a reason: performance. There is concept in computer architectures called data alignment. Every datum has a memory address. The access to a datum is usually faster when there exists a fixed pattern to access the addresses. It makes sense to align addresses by one, four, or eight bytes.
One motive is that all addresses with be multiple of eight (because every byte has eight bits). Assuming addressing with 1 byte, if an address starts at 0, the next starts at 8, then 16, 24, 32, and so son. To find the next value, it suffices to search for the next multiple of eight. If one variable has 4 bytes, it is enough advancing 32 units.
If individual bits were stored, the beginning of each address could be any decimal value. If the first value has 1 bit in an address started at 0, the next value would be at address 1. If the second had 1 byte, the next value would be at address 9. One more bit, address 10. The complexity to identify the address becomes more complex and dependent of what is stored at a given time.
Computer and modern devices may have large amounts of memory. If a machine has gigabytes of RAM, the exchange of a few bits to improve the performance at the cost of memory can be worth. However, this is not always the case.
There are machines with limited amounts of memory (such as a few hundred bytes). This is common, for instance, when one works with embedded circuits. There also exists programs on which performance is essential; in other programs, the optimization for certain parts of the code can be desirable. Even in modern computers and devices, the amount of cache memory is low (normally to a few tens of kilobytes or a couple megabytes). In modern architectures, locality of reference is an important concept for high-performance computing. The closer the data, the higher the changes of accessing the value in a faster memory (such as the cache).
Some programming languages, particularly lower level ones, provide ways of accessing individual bits from a memory region. This is often performed using the integer type. If one thinks about an integer number as a set of bytes, she/he can imagine that each bit of the number is a "sub-variable" of the logic type. This means that 1 byte can store 8 individual logic values; 4 bytes can store 32 logic values; 8 bytes can store 64 logic values. Analogously, a 4 bytes integer can store 2 values of 2 bytes or 4 values of 1 byte each.
At the cost of the complexity of memory manipulation, one can use all bits of the memory.
Bitwise Operations
What one can do you with a bit? The answer is in a previous topic: Logic Operations and Boolean Algebra. In fact, logic gates can define computers.
There are four main logic operations:
Since the introduction of the operation, the first three have been frequently used in previous topics. Bit manipulation has four equivalent operations. To avoid confusion, there are typically prefixed with the term bitwise. Similarly, the four operations for logical (boolean) types can be prefixed by logic.
Bitwise operations also have a unique operation, consisting of shifting bits. The next subsection detail the six typical bitwise operations.
Bitwise Or
From the logical operators' topic, the Logic Or has the following truth table:
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
The bitwise or applies the or operation to each bit of a variable.
In programming languages, the operation is typically represented by a single vertical bar (|).
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| q | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 90 |
| p | q | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 126 |
In the previous table, the following operations are performed:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Therefore, the equivalent of eight logic operations have been performed with a single operation. For variables with more bytes, the same process happens. Thus, for a 4 bytes integer, a single operation performs the equivalent to 32 logic operations. All other bitwise operations work similarly.
It should be noted that each column of the table with the decimal value provides the value that would be written as an integer. However, the interest in bitwise operations is the binary representation of the integer number. Bitwise operations are, therefore, an alternative way of interpreting a binary representation (even if the data type corresponds to a type with another name).
Bitwise And
From the logical operators' topic, the Logic And has the following truth table:
| False | False | False |
| False | True | False |
| True | False | False |
| True | True | True |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The bitwise and applies the and operation to each bit of a variable.
In programming languages, the operation is typically represented by ampersand (&).
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| q | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 90 |
| p | q | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 24 |
In the previous table, the following operations are performed:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Bitwise Not or One's Complement
From the logical operators' topic, the Logic Not has the following truth table:
| False | True |
| True | False |
| 0 | 1 |
| 1 | 0 |
The bitwise not applies the not operation to each bit of a variable.
In programming languages, the operation is typically represented by tilde (~).
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| ~p | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 195 |
In the previous table, the following operations are performed:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Bitwise Exclusive Or (Xor)
From the logical operators' topic, the Logic Xor has the following truth table:
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | False |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The bitwise xor applies the xor operation to each bit of a variable.
In programming languages, the operation is typically represented by a circumflex accent (^).
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| q | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 90 |
| p ^ q | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 102 |
In the previous table, the following operations are performed:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Bit Shift
Besides logic operations, programming languages can provide operators for bit shifting. The principle is simple: move all bits of a number to a direction.
Além das operações lógicas, linguagens de programação podem fornecer operadores para deslocamento de bits.
Strictly speaking, there are types of shifting:
- Arithmetic shift;
- Logical shift;
- Circular shift.
Programming languages typically provide operators for the arithmetic shift. Therefore, they will be commented in the following subsections. If you want to learn about the other types, you can refer to this Wikipedia entry.
Left Shift
The left shift moves all bit stored in a variable by a certain number of positions to the left. In the least significant bit (), the value zero (0) is always introduced. In practice, left shifting is equivalent to multiply a number by 2.
In programming languages, left shift typically is represented by an operator consisting of two less than symbols in sequence (<<).
After the operator, one should provide the number of places to shift.
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p << 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p << 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 120 |
| p << 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 240 |
| p << 3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 224 |
| p << 4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 192 |
| p << 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 128 |
| p << 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
However, as it can be noted in the table, the result of the operation as a multiplication is valid only if:
- The most significant bit (unsigned) is zero;
- The representation of the number has an arbitrary (instead of fixed) number of binary digits.
Otherwise, the resulting value can be smaller than the original one.
This happens in p << 2 and p << 3 in the example.
To obtain the value 480, the variable would need 9 bits; for 960, it would need 10 bits; and so on.
For signed numbers, the shift can modify the sign of the number, depending on the implementation. For instance, for a 1 byte (8 bits) variable assumed as a signed integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p << 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p << 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 120 |
| p << 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | -16 |
| p << 3 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | -32 |
| p << 4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | -64 |
| p << 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -128 |
| p << 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
This happens because, in two's complement, the most significant bit (in this case, ) is used for negative numbers.
Right Shift
The right shift moves all bit stored in a variable by a certain number of positions to the right. In practice, right shifting is equivalent to divide a number by 2.
In programming languages, right shift typically is represented by an operator consisting of two greater than symbols in sequence (>>).
After the operator, one should provide the number of places to shift.
In the most significant bit ( for 1 byte), the introduced value depends on the implementation. In implementations that not preserve the sign of the number, zero is added; the number always will be positive.
For instance, for a 1 byte (8 bits) variable assumed as an unsigned integer:
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p >> 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 60 |
| p >> 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 30 |
| p >> 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 15 |
| p >> 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 7 |
| p >> 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 3 |
| p >> 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| p >> 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
In implementations that preserve the sign, the value of the sign bit is copied and zero is inserted in the second most significant digit. The other digits are shifted normally.
| Variable / Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | Decimal Value |
|---|---|---|---|---|---|---|---|---|---|
| p | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | -60 |
| p >> 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | -60 |
| p >> 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | -30 |
| p >> 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | -15 |
| p >> 3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | -8 |
| p >> 4 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | -4 |
| p >> 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | -2 |
| p >> 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
Bitwise Operations in Programming Languages
The support for bitwise operations vary among programming languages. Lower level languages tend to provide operators. Higher level languages may not provide them.
JavaScript, Python, Lua and GDScript
JavaScript, Python and GDScript are languages that provide predefined bitwise operators.
In Lua, the language provides predefined operators since version 5.3 (documentation).
The version 5.1 of Lua does not provide predefined operators.
The version 5.2 provides a predefined library called bit32 (documentation).
let bitwise_and = 60 & 90
let bitwise_or = 60 | 90
let bitwise_not = ~60
let bitwise_xor = 60 ^ 90
let left_shift = 60 << 1
let right_shift = 60 >> 1bitwise_and = 60 & 90
bitwise_or = 60 | 90
bitwise_not = ~60
bitwise_xor = 60 ^ 90
left_shift = 60 << 1
right_shift = 60 >> 1-- Requires Lua 5.3 or newer.
local bitwise_and = 60 & 90
local bitwise_or = 60 | 90
local bitwise_not = ~60
-- Attenion! Lua uses ~ instead of ^.
local bitwise_xor = 60 ~ 90
local left_shift = 60 << 1
local right_shift = 60 >> 1extends Node
func _init():
var bitwise_and = 60 & 90
var bitwise_or = 60 | 90
var bitwise_not = ~60
var bitwise_xor = 60 ^ 90
var left_shift = 60 << 1
var right_shift = 60 >> 1JavaScript, Python and GDScript also provide combinations of the operators with the assignment operation.
The operators are: &=, |=, ^=, <<= e >>=.
Thus, for instance, x &= y is equivalent to x = x & y.
The languages do not provide an operator for ~= (for bitwise not).
When one works with bitwise operations, it is often more convenient to write values in binary or hexadecimal bases.
When available, writing a number in hexadecimal usually uses the prefix 0x, while writing a number in binary usually uses the prefix 0b.
Some programming languages, such as JavaScript, Python and GDScript, allow writing literals in both bases.
Lua only allows writing hexadecimal values.
console.log(0b111100, 0x3c, 0x3C)
console.log(Number(60).toString(2), Number(60).toString(16))print(0b111100, 0x3c, 0x3C)
print(bin(60), hex(60))print(0x3c, 0x3C)extends Node
func _init():
printt(0b111100, 0x3c, 0x3C)Some programming languages also provide subroutines to convert or write integer values in binary or hexadecimal bases as a string.
JavaScript and Python are two examples.
In JavaScript, Number.toString() (documentation) performs the conversion.
In Python, on can use bin() (documentation) for binary conversion and hex() (documentation) for hexadecimal conversion.
Lua 5.1: Libraries or Creating Your Own Implementation
Lua 5.1 does not provide predefined bitwise operators. There are libraries that provide implementations; this page from lua-users.org provide some suggestions.
If one uses LuaJIT, the implementation provides the library LuaBit out of the box. There also exists a request to add operators to LuaJIT.
Another possibility is creating one's own implementation.
A simple (albeit inefficient) way is converting an integer number to an array that stores zeros and ones to represent the bits of the numbers.
Next, for and, or, not and xor, it suffices using the corresponding logic operation to calculate the result for each index of the array.
For bit shifting, it suffices adding or removing elements from the array.
You can try implementing a solution as an exercise to practice. The next code block provides a possible implementation, based in the explanation from the previous paragraph.
function integer_to_binary(value, number_of_bits)
local result = {}
local sign = 1
if (value >= 0) then
value = math.floor(value)
else
value = math.ceil(value)
sign = -1
end
repeat
table.insert(result, 1, value % 2)
value = value / 2
if (value >= 0) then
value = math.floor(value)
else
value = math.ceil(value)
end
until (value == 0)
if (number_of_bits ~= nil) then
while (#result < number_of_bits) do
table.insert(result, 1, 0)
end
end
return result, sign
end
function binary_to_integer(binary_array, sign)
sign = sign or 1
local result = 0
for _, digit in ipairs(binary_array) do
result = result * 2 + digit
end
return (sign * result)
end
function print_binary(value, number_of_bits)
local binary_value, sign = integer_to_binary(value, number_of_bits)
if (sign < 0) then
io.write("-")
end
io.write("0b")
for _, digit in ipairs(binary_value) do
io.write(digit)
end
io.write("\n")
end
function bitwise_and(x, y, number_of_bits)
number_of_bits = number_of_bits or 32
local binary_x = integer_to_binary(x, number_of_bits)
local binary_y = integer_to_binary(y, number_of_bits)
local result = {}
for index = 1, number_of_bits do
if ((binary_x[index] == 1) and (binary_y[index] == 1)) then
table.insert(result, 1)
else
table.insert(result, 0)
end
end
return result
end
function bitwise_or(x, y, number_of_bits)
number_of_bits = number_of_bits or 32
local binary_x = integer_to_binary(x, number_of_bits)
local binary_y = integer_to_binary(y, number_of_bits)
local result = {}
for index = 1, number_of_bits do
if ((binary_x[index] == 1) or (binary_y[index] == 1)) then
table.insert(result, 1)
else
table.insert(result, 0)
end
end
return result
end
function bitwise_not(x, number_of_bits)
number_of_bits = number_of_bits or 32
local binary_x = integer_to_binary(x, number_of_bits)
local result = {}
for index = 1, number_of_bits do
if (binary_x[index] == 1) then
table.insert(result, 0)
else
table.insert(result, 1)
end
end
return result
end
function bitwise_xor(x, y, number_of_bits)
number_of_bits = number_of_bits or 32
local binary_x = integer_to_binary(x, number_of_bits)
local binary_y = integer_to_binary(y, number_of_bits)
local result = {}
for index = 1, number_of_bits do
if (binary_x[index] ~= binary_y[index]) then
table.insert(result, 1)
else
table.insert(result, 0)
end
end
return result
end
function left_shift(x, number_of_bits)
local result, sign = integer_to_binary(x)
for i = 1, number_of_bits do
table.insert(result, 0)
end
return result, sign
end
function right_shift(x, number_of_bits)
local result, sign = integer_to_binary(x)
for i = 1, number_of_bits do
table.remove(result, #result)
table.insert(result, 1, 0)
end
return result, sign
endIn the example, the most significant digit is stored in the first index of the array (index 1 in Lua); the least significant is stored in the last position.
The solution stores the value of sign of the number separately; the values are compared as unsigned integers.
Alternatively, you could create a representation of sign bit or two's complement in integer_to_binary().
In this case, it would also be necessary to update binary_to_integer() and right_shift().
Show/Hide Usage Examples
for i = -32, 32 do
local binary_value, sign = integer_to_binary(i)
print(binary_to_integer(binary_value, sign))
print_binary(i, 8)
end
print("Bitwise and")
print_binary(0x6, 8)
print_binary(0xF, 8)
print_binary(binary_to_integer(bitwise_and(0x6, 0xF, 8)), 8)
print("Bitwise or")
print_binary(0x6, 8)
print_binary(0xF, 8)
print_binary(binary_to_integer(bitwise_or(0x6, 0xF, 8)), 8)
print("Bitwise not")
print_binary(0x6, 8)
print_binary(binary_to_integer(bitwise_not(0x6, 8)), 8)
print("---")
print_binary(0xF, 8)
print_binary(binary_to_integer(bitwise_not(0xF, 8)), 8)
print("Bitwise xor")
print_binary(0x6, 8)
print_binary(0xF, 8)
print_binary(binary_to_integer(bitwise_xor(0x6, 0xF, 8)), 8)
print("< 4")
print_binary(0x6, 8)
print_binary(binary_to_integer(left_shift(0x6, 4)), 8)
print("---")
print_binary(0xF, 8)
print_binary(binary_to_integer(left_shift(0xF, 4)), 8)
print("> 2")
print_binary(0x6, 8)
print_binary(binary_to_integer(right_shift(0x6, 2)), 8)
print("---")
print_binary(0xF, 8)
print_binary(binary_to_integer(right_shift(0xF, 2)), 8)Examples
If one knows logic operations, she/he may not find many difficulties with bitwise operations. On the other hand, bitwise operations have some interesting uses (although low-level ones). The next subsections present some typical uses of bitwise operations.
Flags and Multiple Properties in a Single Variable
A flag is a value that communicates the presence (or absence) of a property. The use of flags it not new to this topic. For instance, they have been previously used in Command Line Input to define binary parameters.
Bitwise operations allow extending the use of flags. Instead of one variable per property, a single variable can store multiple properties.
const BLACK = 0 // 0
const RED = 1 << 0 // 1
const GREEN = 1 << 1 // 2
const BLUE = 1 << 2 // 4
// Combining properties using a bitwise or.
let red = RED
let yellow = RED | GREEN
let magenta = RED | BLUE
let cyan = GREEN | BLUE
let white = RED | GREEN | BLUE
// Check if a property is enabled using bitwise and.
console.log("Magenta has red?", ((magenta & RED) === RED))
console.log("White has red and green?",
((white & (RED | GREEN)) === (RED | GREEN)))
// Creating a color using the additive model.
let color = BLACK
color |= RED
color |= GREEN
// Removal of property using bitwise and, as well as a bitwise not.
color &= ~GREEN
console.log(color === RED)
// Inversion of bits using bitwise xor.
let complementary_color = color ^ white
console.log(complementary_color === cyan)BLACK = 0 # 0
RED = 1 << 0 # 1
GREEN = 1 << 1 # 2
BLUE = 1 << 2 # 4
# Combining properties using a bitwise or.
red = RED
yellow = RED | GREEN
magenta = RED | BLUE
cyan = GREEN | BLUE
white = RED | GREEN | BLUE
# Check if a property is enabled using bitwise and.
print("Magenta has red?", ((magenta & RED) == RED))
print("White has red and green?",
((white & (RED | GREEN)) == (RED | GREEN)))
# Creating a color using the additive model.
color = BLACK
color |= RED
color |= GREEN
# Removal of property using bitwise and, as well as a bitwise not.
color &= ~GREEN
print(color == RED)
# Inversion of bits using bitwise xor.
complementary_color = color ^ white
print(complementary_color == cyan)local BLACK <const> = 0 -- 0
local RED <const> = 1 << 0 -- 1
local GREEN <const> = 1 << 1 -- 2
local BLUE <const> = 1 << 2 -- 4
-- Combining properties using a bitwise or.
local red = RED
local yellow = RED | GREEN
local magenta = RED | BLUE
local cyan = GREEN | BLUE
local white = RED | GREEN | BLUE
-- Check if a property is enabled using bitwise and.
print("Magenta has red?", ((magenta & RED) == RED))
print("White has red and green?",
((white & (RED | GREEN)) == (RED | GREEN)))
-- Creating a color using the additive model.
local color = BLACK
color = color | RED
color = color | GREEN
-- Removal of property using bitwise and, as well as a bitwise not.
color = color & (~GREEN)
print(color == RED)
-- Inversion of bits using bitwise xor.
local complementary_color = color ~ white
print(complementary_color == cyan)extends Node
const BLACK = 0 # 0
const RED = 1 << 0 # 1
const GREEN = 1 << 1 # 2
const BLUE = 1 << 2 # 4
func _init():
# Combining properties using a bitwise or.
var red = RED
var yellow = RED | GREEN
var magenta = RED | BLUE
var cyan = GREEN | BLUE
var white = RED | GREEN | BLUE
# Check if a property is enabled using bitwise and.
printt("Magenta has red?", ((magenta & RED) == RED))
printt("White has red and green?",
((white & (RED | GREEN)) == (RED | GREEN)))
# Creating a color using the additive model.
var color = BLACK
color |= RED
color |= GREEN
# Removal of property using bitwise and, as well as a bitwise not.
color &= ~GREEN
print(color == RED)
# Inversion of bits using bitwise xor.
var complementary_color = color ^ white
print(complementary_color == cyan)The previous examples illustrate the most common operations using flags:
- Bit verification: use a bitwise and to check whether the bits of a flag are enabled;
- Bit activation: use of a bitwise or to enable bits in a flag;
- Bit deactivation: use of a bitwise and, as well as a a bitwise not to disable bits of a flag;
- Bit inversion: use of a bitwise xor to invert enabled and disabled bits of a flag.
The use of bits in the plural is due to the possibility of combining properties to operate multiple bits in a single operation.
The creation of properties using left bit shifts guarantees that there does not exist conflict between the chosen bits. Each shift generates a different power of 2, representing a specific bit of the variable.
| Color | Red? (+1) | Green? (+2) | Blue? (+4) | Value |
|---|---|---|---|---|
| Black | No | No | No | 0 |
| Red | Yes | No | No | 1 |
| Green | No | Yes | No | 2 |
| Blue | No | No | Yes | 4 |
| Yellow | Yes | Yes | No | 3 |
| Magenta | Yes | No | Yes | 5 |
| Cyan | No | No | No | 6 |
| White | Yes | Yes | Yes | 7 |
As each property belongs to a different bit of a power of 2, the combinations for each property with bitwise operations result in unique values.
Bit Masks for Data Extraction
For bit verification, the value used for the extraction of part of the bits of the analyzed variable is called a bit mask. The goal of the mask is preserving the value of the bits of interest and remove the remaining ones (which means make them zero).
The area of Computer Networks provides a classical application of bit masks: Classless Inter-Domain Routing (CIDR).
To identify classes, one uses a mask in an IPv4 (Internet Protocol Version 4) address.
A IPv4 address has 4 bytes (32 bits).
To make it easier to read it, the address has the format w.x.y.z, on which w, x, y and z numbers between 0 and 255 (the values can be written as an unsigned byte).
Before considering CIDR, it is worth illustrating the concept of masks with an IP address.
For instance, a hypothetical IP address could be 127.123.45.67.
A possible way to store the values is using an array such as [127, 123, 45, 67].
However, it is also possible to store the address as a single 32-bit integer value.
To extract each part of the value, one can use a mask and bit shifting.
To illustrate the approach, the first step is writing the IP address as an integer number.
A simple way to do this is writing the value in hexadecimal.
To do this, one converts each number w, x, y e z of the IP in the corresponding hexadecimal value.
// 127.123.45.67
// address = [127, 123, 45, 67]
// hexadecimal = 7F 7B 2D 43
let ipv4 = 0x7F7B2D43
console.log(ipv4)# 127.123.45.67
# address = [127, 123, 45, 67]
# hexadecimal = 7F 7B 2D 43
ipv4 = 0x7F7B2D43
print(ipv4)-- 127.123.45.67
-- address = {127, 123, 45, 67}
-- hexadecimal = 7F 7B 2D 43
local ipv4 = 0x7F7B2D43
print(ipv4)extends Node
func _ready():
# 127.123.45.67
# address = [127, 123, 45, 67]
# hexadecimal = 7F 7B 2D 43
var ipv4 = 0x7F7B2D43
print(ipv4)With bitwise operations, one can calculate the same value 0x7F7B2D43 (2138778947) differently.
She/he could use left shifts to place each part of the address in the correct bits of ipv4.
// Bits: 31:24 23:16 15:8 7:0
let address = [ 127, 123, 45, 67]
let ipv4 = address[0] << 24
ipv4 += address[1] << 16
ipv4 += address[2] << 8
ipv4 += address[3]
console.log(ipv4)
console.log(ipv4.toString(16))# Bits: 31:24 23:16 15:8 7:0
address = [ 127, 123, 45, 67]
ipv4 = address[0] << 24
ipv4 += address[1] << 16
ipv4 += address[2] << 8
ipv4 += address[3]
print(ipv4)
print(hex(ipv4))-- Bits: 31:24 23:16 15:8 7:0
local address = { 127, 123, 45, 67}
local ipv4 = address[1] << 24
ipv4 = ipv4 + (address[2] << 16)
ipv4 = ipv4 + (address[3] << 8)
ipv4 = ipv4 + (address[4])
print(ipv4)extends Node
func _ready():
# Bits: 31:24 23:16 15:8 7:0
var address = [ 127, 123, 45, 67]
var ipv4 = address[0] << 24
ipv4 += address[1] << 16
ipv4 += address[2] << 8
ipv4 += address[3]
print(ipv4)The value of ipv4 is the same in both implementations.
To extract the value of each part of the IPv4 address, one uses a flag.
To find the value of the flag, she/he uses the value 1 in the bits that she/he wishes to keep and 0 to the ones that she/he is not interested.
Thus, to extract a 1 byte value stored in a 4 bytes value, the first step is creating the mask.
The maximum value of an unsigned integer with 1 byte is 255.
Although it is a usual practice in networks, it can be confusing to work with decimal values in masks.
The value 255 in hexadecimal corresponds to 0xFF.
In binary, 0xFF corresponds to 0b11111111.
This way, it is easier to understand how a mask works: 0 & 1 == 0, and 1 & 1 == 1.
In other words, x & 1 == x, if x has one bit.
The bitwise operation repeats this process for the four bytes of the number.
To extract each part of the address, one creates mask corresponding to the positions of the values of interest:
- The last part of the address (
z) is located in the least significant bits. In this case, she/he can use the mask255or0xFF; - The penultimate part (
y) is located in the following eight bits, or the second byte. This means that the goal is to ignore the first eight bits and retrieve the value of the next eight. To do this, she/he can use0xFF00; - The second part (
x) is on the second most significant byte. In this case, the first less significant two bytes must be ignored. This can be achieved with the mask0xFF0000; - The first part (
w) is stored in the most significant byte. The goal is to ignore the three least significant bytes. In other words, the mask is0xFF000000.
Zeros to the left can be used to pad the number and align all mask values.
The next example aligns the value of ipv4 with the values of the masks, which makes it easier to identify the extracted parted.
let ipv4 = 0x7F7B2D43
let w = ipv4 & 0xFF000000
let x = ipv4 & 0x00FF0000
let y = ipv4 & 0x0000FF00
let z = ipv4 & 0x000000FF
console.log(w, x, y, z)
w >>= 24
x >>= 16
y >>= 8
z >>= 0
console.log(w, x, y, z)ipv4 = 0x7F7B2D43
w = ipv4 & 0xFF000000
x = ipv4 & 0x00FF0000
y = ipv4 & 0x0000FF00
z = ipv4 & 0x000000FF
print(w, x, y, z)
w >>= 24
x >>= 16
y >>= 8
z >>= 0
print(w, x, y, z)local ipv4 = 0x7F7B2D43
local w = ipv4 & 0xFF000000
local x = ipv4 & 0x00FF0000
local y = ipv4 & 0x0000FF00
local z = ipv4 & 0x000000FF
print(w, x, y, z)
w = w >> 24
x = x >> 16
y = y >> 8
z = z >> 0
print(w, x, y, z)extends Node
func _ready():
var ipv4 = 0x7F7B2D43
var w = ipv4 & 0xFF000000
var x = ipv4 & 0x00FF0000
var y = ipv4 & 0x0000FF00
var z = ipv4 & 0x000000FF
printt(w, x, y, z)
w >>= 24
x >>= 16
y >>= 8
z >>= 0
printt(w, x, y, z)The use of a bitwise and allows removing undesirable remaining digits. It is, thus, an example of applying a mask to extract the value.
In the code, it should be noted that one needs to right shift the values to retrieve the expected values.
The number of places is the same value used to create the number; the only difference is that the shift direction has been reversed.
This motivates an alternative way to write the example.
Instead of modifying the mask, the implementation can shift the bits to the right first, to place the expected values in the first byte.
Then, one can apply the same 0xFF mask to extract the value.
let ipv4 = 0x7F7B2D43
let address = []
address.push(ipv4 >> 24)
address.push(ipv4 >> 16 & 0xFF)
address.push(ipv4 >> 8 & 0xFF)
address.push(ipv4 & 0xFF)
console.log(address)ipv4 = 0x7F7B2D43
address = []
address.append(ipv4 >> 24)
address.append(ipv4 >> 16 & 0xFF)
address.append(ipv4 >> 8 & 0xFF)
address.append(ipv4 & 0xFF)
print(address)local ipv4 = 0x7F7B2D43
local address = {}
table.insert(address, ipv4 >> 24)
table.insert(address, ipv4 >> 16 & 0xFF)
table.insert(address, ipv4 >> 8 & 0xFF)
table.insert(address, ipv4 & 0xFF)
print(address[1] .. "." .. address[2] .. "." .. address[3] .. "." .. address[4])extends Node
func _ready():
var ipv4 = 0x7F7B2D43
var address = []
address.append(ipv4 >> 24)
address.append(ipv4 >> 16 & 0xFF)
address.append(ipv4 >> 8 & 0xFF)
address.append(ipv4 & 0xFF)
print(address)The values have been stored in an array to provide a different example.
After the extraction, address stores the values [127, 123, 45, 67].
This happens because the performed operations are the reverse of the those used to create the value.
The application of the reverse operations extract four one byte values stored in a four bytes value.
CIDR Calculator
As a second example, the concept of CIDR can be considered to generate masks for classes.
The localhost address used in Libraries is an example of private network.
In the context of networks, private network means a network that is not public, which implies an internal network that is not part of the Internet.
The default value for localhost is the address 127.0.0.1.
localhost belongs to the address range 127.0.0.0/8, known as loopback private network.
In the address, /8 means that the first 8 bits of the address represent the network address.
The remaining 24 bits identify the host (the identifier machine or device).
The mask to extract the network address bits in the format w.x.y.z/8 is 255.0.0.0, which is called a subnet mask.
The value can be found by adding 8 digits 1 in sequence: 0b11111111 and converting the value to a decimal number.
The value 255 preserves the value of w; each 0 removes the values of x, y and z.
Analogously, the mask to extract the bits for the host of an address in the same format corresponds to 0.255.255.255, which is called a wildcard mask.
Therefore, every address of the loopback private network starts with the value 127, and has the format 127.x.y.z.
The same principle applies to the other intervals.
For instance, 192.168.0.0/16 uses 16 bits for the network address and 16 bits for the host.
If you have ever configured a router in a home network, the beginning of the address may be familiar.
In this case, the subnet mask is 255.255.0.0 (once again, thinking about the hexadecimal value can help to understand the value).
The mask for hosts is 0.0.255.255.
From the two examples, one can notice that the wildcard mask is the bitwise negation of the subnet mask.
If the previous paragraphs are confusing, the ideal approach consists of creating a program to automate the process. The next example illustrates the process for IPv4.
// 127.123.45.67
let address = [127, 123, 45, 67]
// 1--30.
let cidr_bits = 8
let subnet_mask = [0, 0, 0, 0]
let remaining_bits = cidr_bits
let index = 0
while (remaining_bits > 0) {
let considered_bits = Math.min(remaining_bits, 8)
let mask = 256 - Math.pow(2, 8 - considered_bits)
subnet_mask[index] = Math.floor(mask)
remaining_bits -= 8
++index
}
let wildcard_mask = [0, 0, 0, 0]
for (index = 0; index < 4; ++index) {
wildcard_mask[index] = ~subnet_mask[index] & 255
}
let network_address = [0, 0, 0, 0]
let host_address = [0, 0, 0, 0]
for (index = 0; index < 4; ++index) {
network_address[index] = address[index] & subnet_mask[index]
host_address[index] = address[index] & wildcard_mask[index]
}
console.log(network_address, "/", cidr_bits)
console.log("Subnet mask:", subnet_mask)
console.log("Wildcard mask:", wildcard_mask)
console.log("Network address:", network_address)
console.log("Host address in the network:", host_address)# 127.123.45.67
address = [127, 123, 45, 67]
# 1--30.
cidr_bits = 8
subnet_mask = [0, 0, 0, 0]
remaining_bits = cidr_bits
index = 0
while (remaining_bits > 0):
considered_bits = min(remaining_bits, 8)
mask = 256 - 2 ** (8 - considered_bits)
subnet_mask[index] = int(mask)
remaining_bits -= 8
index += 1
wildcard_mask = [0, 0, 0, 0]
for index in range(4):
wildcard_mask[index] = ~subnet_mask[index] & 255
network_address = [0, 0, 0, 0]
host_address = [0, 0, 0, 0]
for index in range(4):
network_address[index] = address[index] & subnet_mask[index]
host_address[index] = address[index] & wildcard_mask[index]
print(network_address, "/", cidr_bits)
print("Subnet mask:", subnet_mask)
print("Wildcard mask:", wildcard_mask)
print("Network address:", network_address)
print("Host address in the network:", host_address)-- 127.123.45.67
local address = {127, 123, 45, 67}
-- 1--30.
local cidr_bits = 8
local subnet_mask = {0, 0, 0, 0}
local remaining_bits = cidr_bits
local index = 1
while (remaining_bits > 0) do
local considered_bits = math.min(remaining_bits, 8)
local mask = 256 - 2 ^ (8 - considered_bits)
subnet_mask[index] = math.floor(mask)
remaining_bits = remaining_bits - 8
index = index + 1
end
local wildcard_mask = {0, 0, 0, 0}
for index = 1, 4 do
wildcard_mask[index] = ~subnet_mask[index] & 255
end
local network_address = {0, 0, 0, 0}
local host_address = {0, 0, 0, 0}
for index = 1, 4 do
network_address[index] = address[index] & subnet_mask[index]
host_address[index] = address[index] & wildcard_mask[index]
end
print(network_address[1] .. "." ..
network_address[2] .. "." ..
network_address[3] .. "." ..
network_address[4], "/", cidr_bits)
print("Subnet mask:", subnet_mask[1] .. "." ..
subnet_mask[2] .. "." ..
subnet_mask[3] .. "." ..
subnet_mask[4])
print("Wildcard mask:", wildcard_mask[1] .. "." ..
wildcard_mask[2] .. "." ..
wildcard_mask[3] .. "." ..
wildcard_mask[4])
print("Network address:", network_address[1] .. "." ..
network_address[2] .. "." ..
network_address[3] .. "." ..
network_address[4])
print("Host address in the network:", host_address[1] .. "." ..
host_address[2] .. "." ..
host_address[3] .. "." ..
host_address[4])extends Node
func _init():
# 127.123.45.67
var address = [127, 123, 45, 67]
# 1--30.
var cidr_bits = 8
var subnet_mask = [0, 0, 0, 0]
var remaining_bits = cidr_bits
var index = 0
while (remaining_bits > 0):
var considered_bits = min(remaining_bits, 8)
var mask = 256 - pow(2, 8 - considered_bits)
subnet_mask[index] = int(mask)
remaining_bits -= 8
index += 1
var wildcard_mask = [0, 0, 0, 0]
for index_mask in range(4):
wildcard_mask[index_mask] = ~subnet_mask[index_mask] & 255
var network_address = [0, 0, 0, 0]
var host_address = [0, 0, 0, 0]
for index_mask in range(4):
network_address[index_mask] = address[index_mask] & subnet_mask[index_mask]
host_address[index_mask] = address[index_mask] & wildcard_mask[index_mask]
printt(network_address, "/", cidr_bits)
printt("Subnet mask:", subnet_mask)
printt("Wildcard mask:", wildcard_mask)
printt("Network address:", network_address)
printt("Host address in the network:", host_address)In the specific case of networks, there are tools to calculate CIDR addresses. With some tweaks, the previous example could also become your own tool.
In the example, the generation of the subnet_mask could use bit shifting instead of a power.
The solution could also use a single 32 bits value for each address and the mask, instead of an array with four integer numbers.
In this case, it would be easier to write the IP address in hexadecimal format, as it has been described in the start of this section.
Case Conversion (Uppercase and Lowercase) in ASCII
In Data Types, it was commented about the ASCII table.
A careful inspection of the uppercase letters from A to Z, and of the lowercase letters from a to z revels a pattern.
The subtraction of the corresponding pair of lowercase and uppercase letter always results 32.
32 is a power of 2 ().
Suspicious.
It is not a coincidence. The choice was made by design, to make it easier to convert cases. To convert an uppercase letter to a lowercase one in ASCII, it suffices to sum 32 to the decimal value of the uppercase character. For the opposite conversion from lowercase to uppercase, it suffices to remove 32 of the value of the lowercase character.
Instead of a sum, it is also possible to perform a bitwise operation.
If the value of the bit 5 is 1, the letter is lowercase.
If it is 0, the letter is uppercase.
The decimal value 32 corresponds to 0x20 in hexadecimal.
let message = "Hello, My Name is Franco!"
let uppercase_message = ""
for (let character of message) {
let ascii_character = character.charCodeAt(0)
if ((ascii_character >= "a".charCodeAt(0)) && (ascii_character <= "z".charCodeAt(0))) {
ascii_character &= ~0x20
}
uppercase_message += String.fromCharCode(ascii_character)
}
let lowercase_message = ""
for (let character of message) {
let ascii_character = character.charCodeAt(0)
if ((ascii_character >= "A".charCodeAt(0)) && (ascii_character <= "Z".charCodeAt(0))) {
ascii_character |= 0x20
}
lowercase_message += String.fromCharCode(ascii_character)
}
console.log(uppercase_message)
console.log(lowercase_message)message = "Hello, My Name is Franco!"
uppercase_message = ""
for character in message:
ascii_character = ord(character)
if ((ascii_character >= ord("a")) and (ascii_character <= ord("z"))):
ascii_character &= ~0x20
uppercase_message += chr(ascii_character)
lowercase_message = ""
for character in message:
ascii_character = ord(character)
if ((ascii_character >= ord("A")) and (ascii_character <= ord("Z"))):
ascii_character |= 0x20
lowercase_message += chr(ascii_character)
print(uppercase_message)
print(lowercase_message)local message = "Hello, My Name is Franco!"
local uppercase_message = ""
for character in string.gmatch(message, ".") do
local ascii_character = string.byte(character)
if ((ascii_character >= string.byte("a")) and (ascii_character <= string.byte("z"))) then
ascii_character = ascii_character & ~0x20
end
uppercase_message = uppercase_message .. string.char(ascii_character)
end
local lowercase_message = ""
for character in string.gmatch(message, ".") do
local ascii_character = string.byte(character)
if ((ascii_character >= string.byte("A")) and (ascii_character <= string.byte("Z"))) then
ascii_character = ascii_character | 0x20
end
lowercase_message = lowercase_message .. string.char(ascii_character)
end
print(uppercase_message)
print(lowercase_message)extends Node
func _init():
var message = "Hello, My Name is Franco!"
var uppercase_message = ""
for character in message:
var ascii_character = ord(character)
if ((ascii_character >= "a".to_ascii()[0]) and (ascii_character <= "z".to_ascii()[0])):
ascii_character &= ~0x20
uppercase_message += PoolByteArray([ascii_character]).get_string_from_ascii()
var lowercase_message = ""
for character in message:
var ascii_character = ord(character)
if ((ascii_character >= "A".to_ascii()[0]) and (ascii_character <= "Z".to_ascii()[0])):
ascii_character |= 0x20
lowercase_message += PoolByteArray([ascii_character]).get_string_from_ascii()
print(uppercase_message)
print(lowercase_message)The functions to convert a character in a string to an ASCII integer have been used in previous topics.
For instance, in Files and Serialization (Marshalling) for the creation of a sound file in WAVE format.
This time, the implementation has also used the reverse function, to convert an integer encoded in ASCII to a string.
In JavaScript, this used String.fromCharCode() (documentation).
In Python, the function is chr() (documentation).
In Lua, this can be performed using string.byte() (documentation).
In GDScript, get_string_from_ascii() (documentation) has been used.
To practice, it is possible to improve the example. Some possibilities include:
- An extraction of the magic number
0x20to a constant; - A calculation of the integer values for
"a","z","A"and"Z", which could, then, be stored in a constant.
To check if a character is uppercase or lowercase, it is also possible to check if the bit with the value 32 is 1.
New Items for Your Inventory
Tools:
- Network calculators.
Skills:
- Use of bitwise operations.
Concepts:
- Bitwise operations:
- Bitwise or;
- Bitwise and;
- Bitwise not;
- Bitwise xor;
- Left bit shift;
- Right bit shift.
- Flags;
- Bit masks.
Programming resources:
- Bitwise operations.
Practice
The color systems RGB and RGBA (previously mentioned in Files and Serialization (Marshalling)) can define colors as 4 byte integers. In RGB, the colors have 256 values of red, green and blue. In RGBA, the colors have 256 values of red, green, blue and alpha (transparency).
With bitwise operations, you can create colors with integer values. There are two popular orders to represent colors in an integer number, which are:
- ARGB32: alpha, red, green, blue;
- RGBA32: red, green blue, alpha.
For more information, you can consult Wikipedia.
Use a bitwise and to check if an integer number is even or odd. Tip: it is enough to check a single bit.
It is possible to implement a swap algorithm using bitwise xor that does not require a temporary variable. If the numbers are different, this can be achieved as a sequence of assignments and three xor operations. Try to find out how.
In the previous exercise, the numbers must be different because
x ^ xalways result zero. In fact, this is a fast way to zero the value of a variable in some implementations of the assembly language. Create a subroutinezero_with_xor()to test the technique.Use a bitwise operation to check whether a letter in ASCII is uppercase. Also try to check if the letter is lowercase with a bitwise variation of the first solution.
Next Steps
Bitwise operations mark the end of the introductory topics of Learn Programming. As it has been mentioned in Files and Serialization (Marshalling), the original plan was to end the material at files. This topic, Command Line Input and Libraries illustrate additional features of programming languages.
The author believes that, at this point, the material covers the main features provided by any programming language. In low-level languages, there are still two omissions: pointers and dynamic memory allocation. These topics require the use of a language such as the C programming language or the C++ programming language. They are important to improve the programming skills, although they have been abstracted in high-level languages.
Besides pointers, techniques for debugging and tests also deserve their own topics. The two themes have been mentioned over some topics. Thus, in the meantime, perhaps the author should create a placeholder topic with links to previous mentions.
Thus, these topics will be analyzed at some time in the future, along with other programming paradigms. In particular, Object-Oriented Programming and Functional Programming are good paradigms to continue the studies.
However, the current plan is starting a material that is more interactive and focused on simulations. The material started in Learn Programming: Introduction and finished in this topic is theoretical. Instead of being restricted to a terminal, it is time to start exploring multimedia resources.
- Introduction;
- Entry point and program structure;
- Output (for console or terminal);
- Data types;
- Variables and constants;
- Input (for console or terminal);
- Arithmetic and basic Mathematics;
- Relational operations and comparisons;
- Logic operations and Boolean Algebra;
- Conditional (or selection) structures;
- Subroutines: functions and procedures;
- Repetition structures (or loops);
- Arrays, collections and data structures;
- Records (structs);
- Files and serialization (marshalling);
- Libraries;
- Command line input;
- Bitwise operations;
- Tests and debugging.
