Learn Programming: Logic Operations and Boolean Algebra
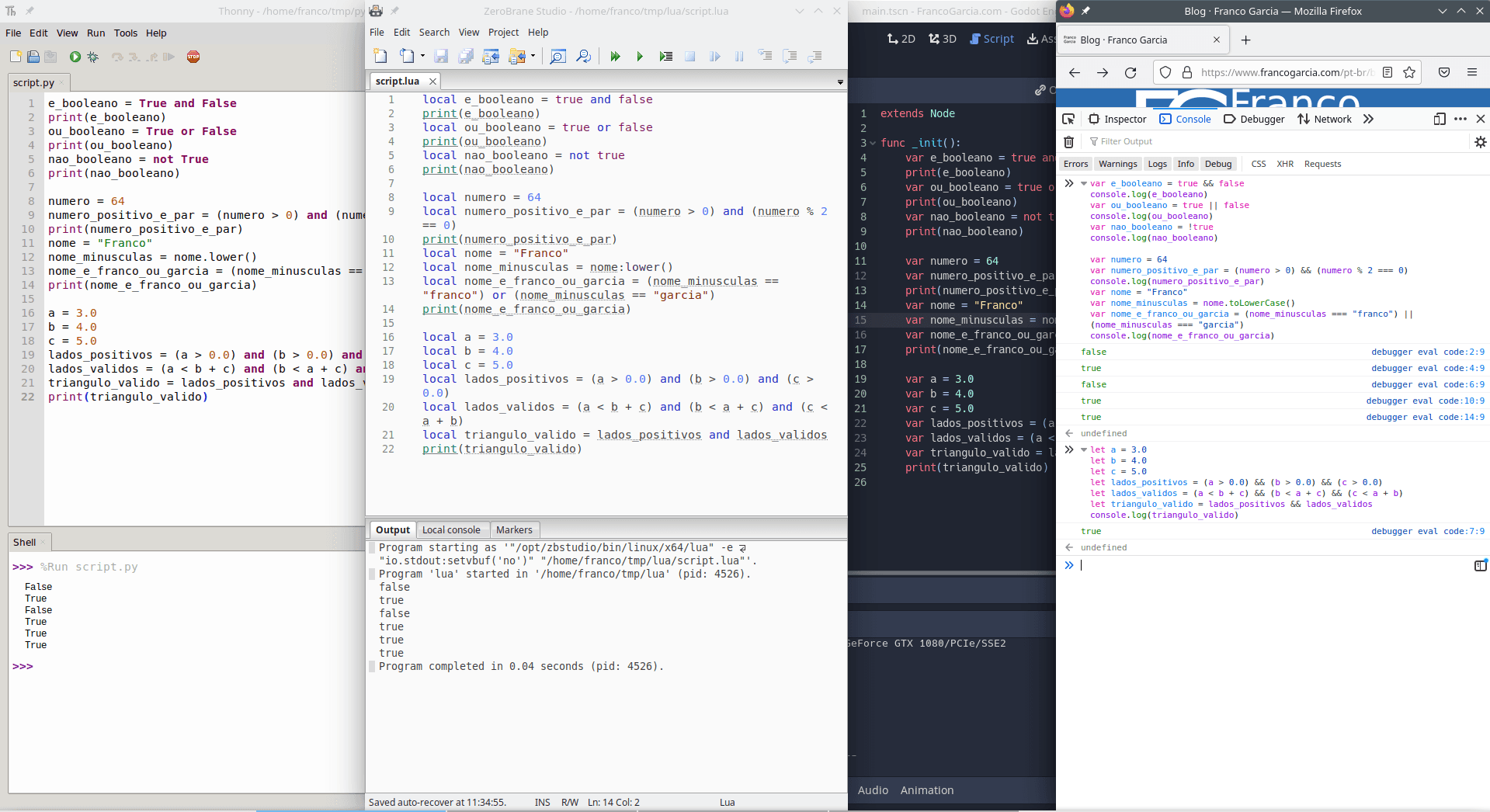
Image credits: Image created by the author using the program Spectacle.
Requirements
In the introduction to development environments, I have mentioned Python, Lua and JavaScript as good choices of programming languages for beginners. Later, I have commented about GDScript as an option for people who want to program digital games or simulations. For the introductory programming activities, you will need, at least, a development environment configured for one of the previous languages.
If you wish to try programming without configuring an environment, you can use of the online editors that I have created:
However, they do not provide all features offered by interpreters for the languages. Thus, sooner or later, you will need to set up a development environment. If you need to configure one, you can refer to the following resources.
Thus, if you have an Integrated Development Environment (IDE), or a combination of text editor and an interpreter, you are ready to start. The following example assumes that you know how to run code in your chosen language, as presented in the configuration pages.
If you want to use another language, the introduction provides links for configure development environments for the C, C++, Java, LISP, Prolog, and SQL (with SQLite) languages. In many languages, it suffices to follow the models from the experimentation section to modify syntax, commands and functions from the code blocks. C and C++ are exceptions, for they require pointers access the memory.
Logic and Arithmetic
As previously commented in Arithmetic and Basic Mathematics, one of components of the processor is called Arithmetic Logic Unit (ALU). The arithmetic part of high-level programming has been previously commented, as well as relational operations for the very first logic results.
Now, it is time to introduce basic logic operations. Although they can also be performed at a lower level, in a bitwise way, this introduction comments about the high level use, by means of logic values and combinations of relation operators.
Boole's Algebra or Boolean Algebra
There are two values in Boole's algebra:
Trueor1;Falseor0.
There are three main operations in boolean algebra:
- Conjunction, also known as
and, which has the symbol (for instance, ); - Disjunction, also known as
or, which has the symbol (for instance, ); - Negation, also known as
not, which has the symbol (for instance, ).
Some languages also define an operator called exclusive-or, at times called xor, which has the symbol (for instance, ).
Logic operations are so frequent that you will likely memorize them from use. Nevertheless, it is always possible to reference the values when they are needed.
Truth Tables
The results of logic operations are summarized in tables called truth tables. A truth table provide the results of a logic expression for every possible combination of logic values for all variables. In other words, if there exists:
- One variable to inspect, the results of an entry for the input
Falseand an entry for the inputTrueare considered; - Two variables: the considered combinations are
False OP False,False OP True,True OP False,True OP True. - Three variables:
OP False False False;OP False False True;OP False True False;OP False True True;OP True False False;OP True False True;OP True True False;OP True True True.
- variables: all the possible combinations of
TrueandFalse.
For programming, the main operators are going to be unary or binary. Thus, they will have 2 or 4 possible results, respectively.
Or
The or operator results True in the case that at least one of the considered values is True.
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
It is important noticing that the logic or does not correspond to the popularly used "or", which normally suggest exclusionary alternatives.
In the logic or, True or True results in True.
For a variation that is closer to the popular meaning, there is the exclusive-or.
For an example of logic or, you can consider the following question: do you like programming or writing?
- If you do not like programming nor writing, the answer is
False; - If you do not like programming, but you do like writing, the answer is
True; - If you like programming, but you do not like writing, the answer is
True; - If you like programming and also do like writing, the answer is
True.
And
The operator and results in True only if both considered operands are True.
In other words, it suffices that the value of one operand is False to make the result of the expression also False.
| False | False | False |
| False | True | False |
| True | False | False |
| True | True | True |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
For an example of logic and, you can consider a similar question to that made for the or: do you like programming or writing?
- If you do not like programming nor writing, the answer is
False; - If you do not like programming, but you do like writing, the answer is
False; - If you like programming, but you do not like writing, the answer is
False; - If you like programming and also do like writing, the answer is
True.
Not
The not operator invests the logic value provided as input.
True results in False; False results in True.
| False | True |
| True | False |
| 0 | 1 |
| 1 | 0 |
For an example of logic not, you can consider a similar question to that made for the or: do you not like programming or writing?
- If you like programming, the answer is
False, because the result is inverted. This can be somewhat confusing. The reason is that, in this case, the variable islike_programming. If you like programming,like_programming = True. Thus,not like_programming == False, for it is the inverted result oflike_programming. - If you do not like programming, the answer is
True.
Questions using not are confusing for daily life, though they will be useful for programming.
To ease the interpretation, you can image that you are asking the opposite you what you want to know.
As in the example, it is also possible to think in the answer for the affirmative version of the question (as an intermediate result in a variable), and invert the answer.
Xor
The operator xor is a variation of ou for which the result is True only when the operands have different values.
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | False |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The expression is logically equivalent () to:
In pseudocode: p xor q == ((p or q) and (not (p and q))).
Therefore, if a programming language does not provide a xor operator, it is possible to create an equivalent expression using the previous pseudocode.
For an example of logic xor, you can consider a similar question to that made for the or: do you like programming or writing, though you do like both?
- If you do not like programming nor writing, the answer is
False; - If you do not like programming, but you do like writing, the answer is
True; - If you like programming, but you do not like writing, the answer is
True; - If you like programming and also do like writing, the answer is
False.
Logical Equivalences
A logical equivalence corresponds to an expression that can be swapped for another maintaining all the same results. In other words, both expressions of a logical equivalence have the same truth table.
The following table summarizes the main logical equivalences.
| Nome | Expressão | Expressão Equivalente |
|---|---|---|
| Double negation | not not p | p |
| Identity | p and True | p |
p or False | p | |
| Domination | p and False | False |
p or True | True | |
| Idempotency | p and p | p |
p or p | p | |
| Negation | p and (not p) | False |
p or (not p) | True | |
| Commutativity | p and q | q and p |
p or q | q or p | |
| Associativity | (p and q) and r | p and (q and r) |
(p or q) or r | p or (q or r) | |
| Distribute property | (p and q) or (p and r) | p and (q or r) |
(p or q) and (p or r) | p or (q and r) | |
| Absorption | p and (p or q) | p |
p or (p and q) | p | |
| De Morgan's laws | (not p) and (not q) | not (p or q) |
(not p) or (not q) | not (p and q) |
It is worth noting that many are similar to equivalences used in Mathematics for arithmetic operations.
The table allows generating simpler (or alternative) equivalent expressions.
For instance, it is redundant to write p or True, because True is always True; thus, the or result will always be True, making the p superfluous.
In fact, the logical equivalence named domination expresses that same result.
Similarly, p or False is equivalent to writing only p (due to the identity), because False will always be False.
Because of the or operator, the result will always depend on p.
If p is True, the expression will result True.
Otherwise, the result will be False.
In case of doubts if you wish to understand the equivalences, you can write the truth table for each expression. Another alternative is writing a code to analyze the results (and, if you wish, compare them automatically with relational operations).
The previous relations are the most usual in programming, although there exists more. There are also logical inferences; as a curiosity, one of the most famous logical inferences rules is called modus ponens.
Logic Gates
Computers work by means of logic operations. Besides the proper logic operations for logic itself, logic operators allow computers to perform arithmetic operations. As incredible as it may seem, computer memory can also be defined using logic operations.
In other words, it is possible to build computers using only logic operations. For commodity, there are ready to use circuits to build digital devices called logic gates.
Computer memory can be created, for example, as combinations of the logic gates not and and (or with a combination of both, called NAND gate); it is also possible to create it using the logic gates not and or (or with the combination, called NOR gate).
If you want to learn more, search for flip-flop.
If you wish to learn more about how computers perform Math operations using logic operations, a good start is to learn about a adder circuit, which can add bits.
Logic Operators in Programming
Programming activities usually are not low level enough to operate with logic gates, although it is possible. There are programming languages to specify hardware, that allows to create complex circuits as combinations of simpler ones (that, in the lowest level, are combinations of logic gates).
Although it can be interesting, the use of logic operations in programming languages for software is much simpler.
Flowcharts: Flowgorithm
As it happened with relation operators, logic operators in Flowgorithm At this time, they can be used in Assign or in Output.
Logic values in Flowgorithm are true and false.
Flowgorithm defines and or && for the logic operator and; or or ||, for the logic operator ou; not or !, for the logic operator not.
You can choose the one you prefer; the names will adopt the written names.

The following code snippet contains the transcription of the text in the image.
Main
Boolean booleanAnd
booleanAnd = true and false
Output booleanAnd
Boolean booleanOr
booleanOr = true or false
Output booleanOr
Boolean booleanNot
booleanNot = not true
Output booleanNot
Integer number
number = 64
Boolean positiveAndEvenNumber
positiveAndEvenNumber = (number > 0) and (number % 2 == 0)
Output positiveAndEvenNumber
String lowercaseName
lowercaseName = "Franco"
Boolean isNameFrancoOrGarcia
isNameFrancoOrGarcia = (lowercaseName == "franco") or (lowercaseName == "garcia")
Output isNameFrancoOrGarcia
EndAs Flowgorithm does not provide a subroutine for case conversion, the program assumes the use of lowercase letters for the name.
Visual Programming Language: Scratch
In Scratch, logic operators are in the sidebar Operators, available in the blocks _ and _, _ or _, and not _.
A limitation of the language is the lack of constants for the logic values True and False.
However, as many logic values result from relation operators, the limitation is not always a problem for learning.
An alternative is using an empty not _ block as True, and use an empty _ and _ as False.
The alternative works because, in Scratch, an empty not _ block results true, while an empty _ and _ block results false.
The use can be confusing and (admittedly) it is a workaround, though it works for simple programs for purposes of examples.
Unfortunately, it does work to create a variable called True and a variable called False to store the results of the expressions, because the blocks with logic operators do not use the direct use of variables.
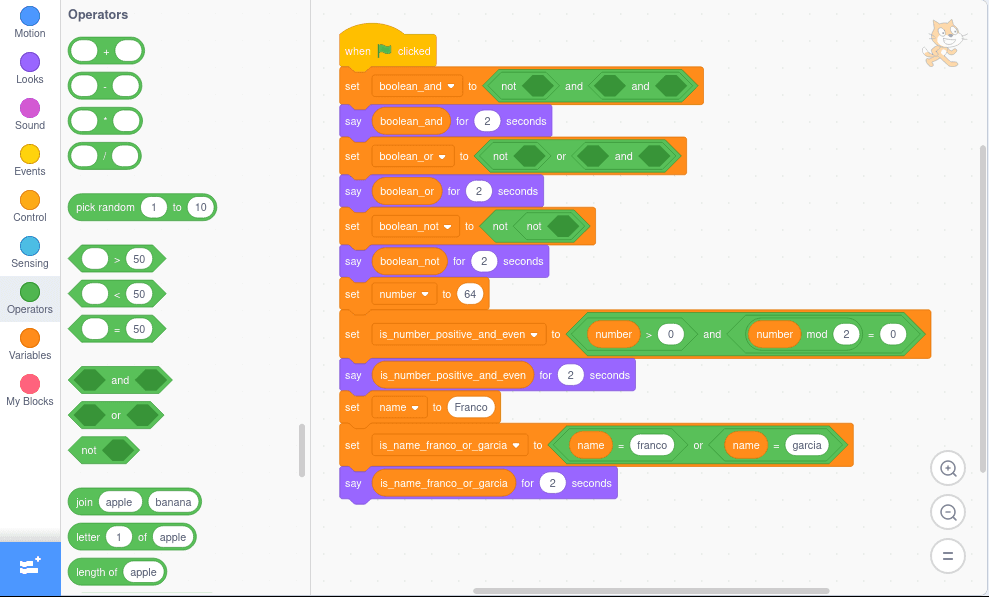
As Scratch is not case-sensitive, the implementation does not convert the name to lowercase for comparison.
Textual Programming Languages: JavaScript, Python, Lua and GDScript
JavaScript provides && for and, || for or, and ! for not.
Python and Lua define and for e, or for ou, and not for not.
GDScript allows to use both styles; you can choose the one you prefer.
Personally, I think it is faster to type the name than use the symbols, though it is a matter of preference.
var boolean_and = true && false
console.log(boolean_and)
var boolean_or = true || false
console.log(boolean_or)
var boolean_not = !true
console.log(boolean_not)
var number = 64
var positive_and_even_number = (number > 0) && (number % 2 === 0)
console.log(positive_and_even_number)
var name = "Franco"
var lowercase_name = name.toLowerCase()
var is_name_franco_or_garcia = (lowercase_name === "franco") || (lowercase_name === "garcia")
console.log(is_name_franco_or_garcia)boolean_and = True and False
print(boolean_and)
boolean_or = True or False
print(boolean_or)
boolean_not = not True
print(boolean_not)
number = 64
positive_and_even_number = (number > 0) and (number % 2 == 0)
print(positive_and_even_number)
name = "Franco"
lowercase_name = name.lower()
is_name_franco_or_garcia = (lowercase_name == "franco") or (lowercase_name == "garcia")
print(is_name_franco_or_garcia)local boolean_and = true and false
print(boolean_and)
local boolean_or = true or false
print(boolean_or)
local boolean_not = not true
print(boolean_not)
local number = 64
local positive_and_even_number = (number > 0) and (number % 2 == 0)
print(positive_and_even_number)
local name = "Franco"
local lowercase_name = name:lower()
local is_name_franco_or_garcia = (lowercase_name == "franco") or (lowercase_name == "garcia")
print(is_name_franco_or_garcia)extends Node
func _init():
var boolean_and = true and false # or true && false
print(boolean_and)
var boolean_or = true or false # true || false
print(boolean_or)
var boolean_not = not true # or !true
print(boolean_not)
var number = 64
var positive_and_even_number = (number > 0) and (number % 2 == 0)
print(positive_and_even_number)
var name = "Franco"
var lowercase_name = name.to_lower()
var is_name_franco_or_garcia = (lowercase_name == "franco") or (lowercase_name == "garcia")
print(is_name_franco_or_garcia)Examples
Logic operators are simply when individually considered. When combined, they allow solving more complex programs, that could be possible without them.
Combining Logic Values
For instance, it is not always possible to relate multiple variables without a logic operator. At times, it is possible for Physics or Math formulas, though what should be done for other problems?
I like...
People normally have more than one interest. What do you like? What do you dislike?
True or false? Do you like:
- Pizza?
- Chocolate?
- Programming?
- Dogs?
- Cats?
The previous questions can be combined to learn more about yourself. For instance, how could inform a computer whether you:
- Like pizza and chocolate?
- Like chocolate or programming?
- Like pizza and dogs, but you do not like cats?
- Like programming or cats, though you do not cats or pizza? This last question can be ambiguous. Programming does not allow ambiguities. Consider it as "but you do not (like cats or pizza)" instead of "but you (do not like dogs) or like pizza".
The answers require the use of logic operators. Modify the values of the variables and discover the answers. With five variable definitions, it is possible to create many combinations of interests.
let like_pizza = false
let like_chocolate = false
let like_programming = false
let like_dogs = false
let like_cats = false
console.log("Do you like pizza and chocolate? ", like_pizza && like_chocolate)
console.log("Do you like chocolate or programming? ", like_chocolate || like_programming)
console.log("Do you like pizza and dogs, but don't you like cats? ", (like_pizza && like_dogs) && (!like_cats))
console.log("Do you like programming or cats, but don't you like dogs or pizza? ", (like_programming || like_cats) && (!(like_dogs || like_pizza)))like_pizza = False
like_chocolate = False
like_programming = False
like_dogs = False
like_cats = False
print("Do you like pizza and chocolate? ", like_pizza and like_chocolate)
print("Do you like chocolate or programming? ", like_chocolate or like_programming)
print("Do you like pizza and dogs, but don't you like cats? ", (like_pizza and like_dogs) and (not like_cats))
print("Do you like programming or cats, but don't you like dogs or pizza? ", (like_programming or like_cats) and (not (like_dogs or like_pizza)))local like_pizza = false
local like_chocolate = false
local like_programming = false
local like_dogs = false
local like_cats = false
print("Do you like pizza and chocolate? ", like_pizza and like_chocolate)
print("Do you like chocolate or programming? ", like_chocolate or like_programming)
print("Do you like pizza and dogs, but don't you like cats? ", (like_pizza and like_dogs) and (not like_cats))
print("Do you like programming or cats, but don't you like dogs or pizza? ", (like_programming or like_cats) and (not (like_dogs or like_pizza)))extends Node
func _init():
var like_pizza = false
var like_chocolate = false
var like_programming = false
var like_dogs = false
var like_cats = false
print("Do you like pizza and chocolate? ", like_pizza and like_chocolate)
print("Do you like chocolate or programming? ", like_chocolate or like_programming)
print("Do you like pizza and dogs, but don't you like cats? ", (like_pizza and like_dogs) and (not like_cats))
print("Do you like programming or cats, but don't you like dogs or pizza? ", (like_programming or like_cats) and (not (like_dogs or like_pizza)))The example show how logic operators allow building more complex expressions to make statements about the state of a program.
Arithmetic, Relational and Logic Operators
To draw conclusions about multiple arithmetic values, relational and logic operators can be used together. Both relational and logic operators provide logic values as answers.
For an example, one can consider the triangle inequality. The triangle inequality affirm that the size of side of a triangle is always smaller than the sum of the other two sides.
In symbols, for a triangle with sides , and :
- ;
- ;
- .
Given three sides, do they form a triangle? You can write a program to answer the question, by processing provided values for the sides.
let a = 3.0
let b = 4.0
let c = 5.0
let valid_triangle = (a < b + c) && (b < a + c) && (c < a + b)
console.log(valid_triangle)a = 3.0
b = 4.0
c = 5.0
valid_triangle = (a < b + c) and (b < a + c) and (c < a + b)
print(valid_triangle)local a = 3.0
local b = 4.0
local c = 5.0
local valid_triangle = (a < b + c) and (b < a + c) and (c < a + b)
print(valid_triangle)extends Node
func _init():
var a = 3.0
var b = 4.0
var c = 5.0
var valid_triangle = (a < b + c) and (b < a + c) and (c < a + b)
print(valid_triangle)How about improving the solution? Sides must be positive numbers.
To ensure that the answer does only admit positive values for each side, it is possible to verify each of them using a comparison (for instance, a > 0) and combine the answers using the and operator.
Next, it suffices to combine the verification of positive sides with the verification of lengths (sizes).
If both results are true, the answer will be True.
If any of the results is False, the answer will be False -- therefore, the sides cannot make a triangle.
let a = 3.0
let b = 4.0
let c = 5.0
let positive_sides = (a > 0.0) && (b > 0.0) && (c > 0.0)
let valid_sides = (a < b + c) && (b < a + c) && (c < a + b)
let valid_triangle = positive_sides && valid_sides
console.log(valid_triangle)a = 3.0
b = 4.0
c = 5.0
positive_sides = (a > 0.0) and (b > 0.0) and (c > 0.0)
valid_sides = (a < b + c) and (b < a + c) and (c < a + b)
valid_triangle = positive_sides and valid_sides
print(valid_triangle)local a = 3.0
local b = 4.0
local c = 5.0
local positive_sides = (a > 0.0) and (b > 0.0) and (c > 0.0)
local valid_sides = (a < b + c) and (b < a + c) and (c < a + b)
local valid_triangle = positive_sides and valid_sides
print(valid_triangle)extends Node
func _init():
var a = 3.0
var b = 4.0
var c = 5.0
var positive_sides = (a > 0.0) and (b > 0.0) and (c > 0.0)
var valid_sides = (a < b + c) and (b < a + c) and (c < a + b)
var valid_triangle = positive_sides and valid_sides
print(valid_triangle)Alternative Technique
Before proceeding, there is an interesting alternative technique to solve the problem. You can modify the solution slightly and calculate new logic values based on the previous results, as performed for arithmetic calculations. For instance, in JavaScript:
let a = 3.0
let b = 4.0
let c = 5.0
let valid_triangle = a > 0.0
valid_triangle = valid_triangle && (b > 0.0)
valid_triangle = valid_triangle && (c > 0.0)
valid_triangle = valid_triangle && (a < b + c)
valid_triangle = valid_triangle && (b < a + c)
valid_triangle = valid_triangle && (c < a + b)
console.log(valid_triangle)In this case, the result was calculated step by step by updating the value of the last answer, using the last answer's value to include the new check.
Some programming languages, such as JavaScript, even provide a specialized assignment operator to perform the last operation, as &&= (there also exists one for or: ||=, although there does not exist one for the not, because the operator corresponds to the one for difference).
let a = 3.0
let b = 4.0
let c = 5.0
let valid_triangle = a > 0.0
valid_triangle &&= (b > 0.0)
valid_triangle &&= (c > 0.0)
valid_triangle &&= (a < b + c)
valid_triangle &&= (b < a + c)
valid_triangle &&= (c < a + b)
console.log(valid_triangle)The code is a bit strange and not very usual, though it is equivalent to the previous examples.
It should be noted, nevertheless, that if the expression mixed and, or and not, the solution would become more complex, because it must consider every correct grouping and rules of operator's precedence.
Thus, although it is possible, I would recommend following the original implementation (for instance, using positive_sides, valid_sides and valid_triangle) for a solution that is easy to write and understand.
After the introduction of conditional structures, it will be even possible to write it another way.
Building a Truth Table
To create a truth table, one can use a programming language to compute every possible result of a logic expression.
console.log("false && false: ", false && false)
console.log("false && true: ", false && true)
console.log("true && false: ", true && false)
console.log("false && false: ", true && true)
console.log("false || false: ", false || false)
console.log("false || true: ", false || true)
console.log("true || false: ", true || false)
console.log("false || false: ", true || true)
console.log("! false:", !false)
console.log("! true:", !true)print("False and False: ", False and False)
print("False and True: ", False and True)
print("True and False: ", True and False)
print("False and False: ", True and True)
print("False or False: ", False or False)
print("False or True: ", False or True)
print("True or False: ", True or False)
print("False or False: ", True or True)
print("not False:", not False)
print("not True:", not True)print("false and false: ", false and false)
print("false and true: ", false and true)
print("true and false: ", true and false)
print("false and false: ", true and true)
print("false or false: ", false or false)
print("false or true: ", false or true)
print("true or false: ", true or false)
print("false or false: ", true or true)
print("not false:", not false)
print("not true:", not true)extends Node
func _init():
print("false and false: ", false and false)
print("false and true: ", false and true)
print("true and false: ", true and false)
print("false and false: ", true and true)
print("false or false: ", false or false)
print("false or true: ", false or true)
print("true or false: ", true or false)
print("false or false: ", true or true)
print("not false:", not false)
print("not true:", not true)
print("false && false: ", false && false)
print("false && true: ", false && true)
print("true && false: ", true && false)
print("false && false: ", true && true)
print("false || false: ", false || false)
print("false || true: ", false || true)
print("true || false: ", true || false)
print("false || false: ", true || true)
print("! false:", !false)
print("! true:", !true)After the introduction of repetition structures (loops), the process can be even automatized.
Test of Logic Equivalence
When it was commented about the xor operator, a logical equivalence using or, and and not was provided.
How about creating a truth table to verify whether, in fact, ?
console.log("p xor q = ?")
let p = false
let q = false
let xor = ((p || q) && (!(p && q)))
console.log(p, " xor ", q, " = ", xor)
q = true
xor = ((p || q) && (!(p && q)))
console.log(p, " xor ", q, " = ", xor)
p = true
q = false
xor = ((p || q) && (!(p && q)))
console.log(p, " xor ", q, " = ", xor)
q = true
xor = ((p || q) && (!(p && q)))
console.log(p, " xor ", q, " = ", xor)print("p xor q = ?")
p = False
q = False
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = True
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
p = True
q = False
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = True
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)print("p xor q = ?")
local p = false
local q = false
local xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = true
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
p = true
q = false
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = true
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)extends Node
func _init():
print("p xor q = ?")
var p = false
var q = false
var xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = true
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
p = true
q = false
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)
q = true
xor = ((p or q) and (not (p and q)))
print(p, " xor ", q, " = ", xor)It should be noted that variables that were not modified keep their last assigned value. Thus, the result of program will resemble an output like:
p xor q = ?
false xor false = false
false xor true = true
true xor false = true
true xor true = falseIf one compares the result of every line with the corresponding entry of the table, one can observe that, in fact, both expressions are equivalent.
New Items for Your Inventory
Tools:
- Truth tables.
Skills:
- Use of conjunctions;
- Use of disjunctions;
- Use of negations;
- Creation of logic expressions.
Concepts:
- Conjunctions or
and; - Disjunctions or
or; - Negation or
not; - Logical equivalences.
Programming resources:
- Logic operators.
Practice
Create a variable called
fruit. Assign a value to it or request the input of a name for the fruit. Is thefruita banana, apple or grape?In the previous exercise, is the
fruitnot a banana, apple or grape?Create a variable called
number. Is the number odd? Is the number odd and is it equal to 7? Is the number odd and negative? Is the number odd, positive and multiple of 17? Is the number 4? If it is not, is it negative and multiple of 3?Create variables that store logic values with your interests. For instance, whether I like:
- Studying;
- Cooking;
- Sports;
- Programming;
- Games;
- Chats.
Create logic expressions as combinations of variables.
Define four variables for access' credentials:
- Expected username;
- Expected password for the previous username;
- Provided username;
- Provided password.
With the provided date, could the person access the system? That is, would the access be granted for her/him?
Create some variables with grades from 0.0 to 10.0 for books, movies, songs, games, programming languages, or any other item of your interest. Then, verify which items would have average grades, assuming that the average grade is defined as between 5.0 (inclusive) and less than 6.5 (not inclusive) -- that is, the grade belongs to the interval [5.0, 6.5[ (read as closed for 5.0, open to 6.5).
For instance, a movie with the grade 5.0 would be classified as average. So would a music with grade 6.21, as well as a book classified with 6.4999999. A game with grade 6.5 would be considered as average.
For the previous exercise, now consider that:
- Items with grades between [0.0, 5.0[ are classified as poor;
- Items with grades between [6.5, 8.0[ are classified as good;
- Items with grades between [8.0, 10.0] are classified as great.
Choose some combinations of variables and combine them with logic operations. For instance, assuming that your variables include grades for the languages
flowgorithm,scratch,python,lua,javascript, andgdscriptdescribed in this page:- Are any of the previous variable considered great?
flowgorithmorscratchare average?javascript,pythonandluaare good?luais good, average or great?luais not poor?- (
flowgorithmorlua) are (good or great), but (scratchandjavacript) are (poor or average)? - Does there not exist any poor item?
Next Steps
With input, output, arithmetic, relational and logic operation it already is possible to solve some simple problems. With the next concepts, it will become possible to solve problems that are increasingly more complex, with input validation and more sophisticated output.
In particular, every program up to this point was executed linearly; in other words, the machine followed the instructions in the defined order, without skipping any of them.
With conditional structures, it will become possible to choose instructions to run or ignore according to the current state of the program. To do this, relational and logic operatios will define conditions to select the next path to follow.
- Introduction;
- Entry point and program structure;
- Output (for console or terminal);
- Data types;
- Variables and constants;
- Input (for console or terminal);
- Arithmetic and basic Mathematics;
- Relational operations and comparisons;
- Logic operations and Boolean Algebra;
- Conditional (or selection) structures;
- Subroutines: functions and procedures;
- Repetition structures (or loops);
- Arrays, collections and data structures;
- Records (structs);
- Files and serialization (marshalling);
- Libraries;
- Command line input;
- Bitwise operations;
- Tests and debugging.
